dynamicskillingme
- 26
- 0
Homework Statement
Has solution
It then goes on to state the solution blows up at
My issue is when I do the solution I get
(Working)
dynamicskillingme said:\dot{y} = y^2
y = yt + c ; for t = 0
dynamicskillingme said:Homework Statement
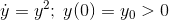
Has solution
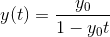
It then goes on to state the solution blows up at, which I understand.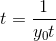
My issue is when I do the solution I get
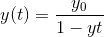
(Working)
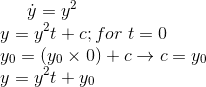
dynamicskillingme said:How could I prove their answer, or what should I read up on to be able to show this proof?