Loop Feynman diagram contributions to correlation functions

[JD_PM]

Homework Statement

Given a quantum field theory whose potential is given by



$$V(\phi) = g \frac{\phi^3}{3!} + \lambda \frac{\phi^4}{4!}$$



Find all connected one and two-loop graphs (to do so you will need to find all symmetry factors involved) which contribute to



\begin{equation*}

\langle \phi(x_1) \phi(x_2) \rangle, \qquad \langle \phi(x_1) \phi(x_2) \phi(x_3)\rangle

\end{equation*}

Relevant Equations

N/A

My understanding of the n-correlation function is

\begin{equation*}
\langle \phi(x_1) \phi(x_2) ... \phi(x_n)\rangle = i \Delta_F (x_1-x_2-...-x_n)
\end{equation*}

Where $\Delta_F$ is known as the Feynman propagator (in Mathematics is better known as Green's function).

Let us analyze $\langle \phi(x_1) \phi(x_2) \rangle$ first. Conventionally, the $\Delta_F(x_1−x_2)$ propagator is drawn as a line

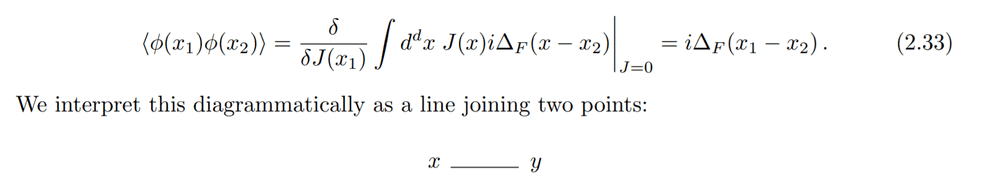
OK. But then I see that the second contribution is given by a diagram with a 'bubble' in between, with a symmetry factor of $2$ attached to it

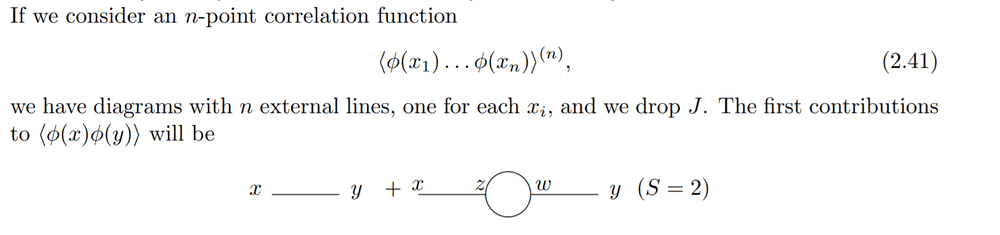
Regarding the symmetry factor $S=2$ attached to the bubble diagram.

This is how I approached it (highly inspired by the accepted answer here) : Let's start with the external leg on the left. There are two possibilities for this external leg to attach: it can attach to either $z$ or $w$. The right external leg is thus left with only one possibility. Hence we have a $2 \times 1$ factor. We could start from right to left instead so, by the same token, we pick up another $2 \times 1$ factor. The upper internal leg can either attach to $z$ or $w$ while the lower is left with one option only; we hence pick up a $2 \times 1$ factor. We could start with the lower internal leg instead so, by the same token, we pick up another $2 \times 1$ factor (still thinking about the argument used for the internal legs...).

Overall, the Dyson series gives us a $1/2!$ factor and the two vertices give $1/(2!2!)$ so the symmetry factor I get is

$$\frac{2\times 1 \times 2\times 1 \times 2\times 1 \times 2\times 1}{2!2!2!}=2$$
My doubts are

1) Why does this 'bubble' contribution emerge?

2) What are the specific Feynman rules that allow us to write down all contributions?

Once I fully understand how $\langle \phi(x_1) \phi(x_2) \rangle$ works, I should be able to show all contributions for $\langle \phi(x_1) \phi(x_2) \phi(x_3) \rangle$

@vanhees71 @Gaussian97 , might you have time to discuss this one?

Thank you

Source: Osborn notes

PS: $\phi^3+\phi^4$ theory was discussed in this enlightening thread.

 

[vanhees71]

Somehow the time-ordering symbol is missing. The Feynman diagrams are just a very clever notation to evaluate the functional derivatives wrt. the external source $J(x)$ or, equivalently, the application of the Wick theorem to evaluate vacuum expectation values of time-ordered field-operator products in the operator formalism. In this way you can also find a safe way to get the symmetry factors. For you one-loop contribution of the four-point function you start with drawing the two three-leg vertices and the two external points. Now you count in how many ways you connect these elements to the diagram of the given topology: for the first external point you have 6 possibilities to connect it with one of the legs. For the 2nd external point you have 3 remaining possibilities. Then you have 2 possibilities to connect one of the legs of one vertex with one of the other. The remaining connection is then unique. So the overall factor is 6*3*2/(3! 3! 2)=1/2.

 

[JD_PM]

@vanhees71 my apologies for the late reply.

For you one-loop contribution of the four-point function you start with drawing the two three-leg vertices and the two external points. Now you count in how many ways you connect these elements to the diagram of the given topology: for the first external point you have 6 possibilities to connect it with one of the legs. For the 2nd external point you have 3 remaining possibilities. Then you have 2 possibilities to connect one of the legs of one vertex with one of the other. The remaining connection is then unique. So the overall factor is 6*3*2/(3! 3! 2)=1/2.

I have been studying this particular case ($\phi^3 \ \& \ \phi^4$ combined) and realized I lack of the basic understanding on how the whole machinery works.

So let me step back, discuss and understand the simplest case I could find: the two-point function.

I want to understand how to construct the Feynman rules for this case (the first non-trivial contribution has been shown in the OP: a bubble diagram with two external legs)

We start off by defining the functional integral

\begin{equation*}
Z[J] = \int d[\phi] e^{iS[\phi] + i\int d^d x J(x) \phi(x)}
\end{equation*}

Which can be rewritten as

\begin{align*}
Z[J] &= \exp\left(\frac{i}{2} \int d^d x d^d y \frac{\delta}{\delta \phi(x)} \Delta_F (x-y) \frac{\delta}{\delta \phi(y)}\right) \times \\
&\times \exp\left( i \int d^d x (-V(\phi(x))+J(x)\phi(x))\right) \Big|_{\phi=0}
\end{align*}

Then Osborn says "expand this to get the perturbation expansion", from which you can construct the Feynman rules. I am trying to see how.

Let's sketch it. If we were to expand it we would get $Z[J] = e^xe^y = 1+ xy + \frac 1 4 (xy)^2 + ...$ but how does this lead to construct the Feynman diagrams?

PS: I am following (the attached) Osborn notes, section 2.2

 

[JD_PM]

Alright, I think I will post a more basic conceptual question and then come back to this particular exercise