Feynman Rules on ##\phi^3, \phi^4## theory

[JD_PM]

Homework Statement:

Given the Lagrangian density

\begin{equation*}
\mathcal{L}=\mathcal{L}_0 + \mathcal{L}_I=\frac 1 2 \partial_{\mu} \phi \partial^{\mu} \phi - \frac{m^2}{2} \phi^2 - \frac{\lambda_3}{3!} \phi^3 - \frac{\lambda_4}{4!} \phi^4
\end{equation*}

Where

\begin{equation*}
\mathcal{L}_0 = \frac 1 2 \partial_{\mu} \phi \partial^{\mu} \phi - \frac{m^2}{2} \phi^2
\end{equation*}

\begin{equation*}
\mathcal{L}_I = - \frac{\lambda_3}{3!} \phi^3 - \frac{\lambda_4}{4!} \phi^4
\end{equation*}


a) Derive what are the interaction vertices of this theory.



b) Determine the Feynman rules for the vertices. Hint: the combinatorics

will not be trivial.

Relevant Equations:

Please see below

Let us first take the S-matrix expansion (i.e. Dyson's formula)

\begin{align*}
S_{fi}&=\langle f | T \left\{ \exp\left( i\frac{\lambda_3}{3!}\int d^4 x :\phi \phi \phi (x) : + i\frac{\lambda_4}{4!}\int d^4 x :\phi \phi \phi \phi (x) : \right) \right\}| i \rangle \\
&= \langle f | i \rangle + i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi \phi \phi (x): |i \rangle + i\frac{\lambda_4}{4!} \int d^4 x \langle f | :\phi \phi \phi \phi (x) : | i \rangle \\
&+ \left(\frac{i\lambda_3}{3!}\right)^2\frac{1}{2!} \int d^4 x d^4 y \langle f| T\left\{ : \phi \phi \phi (x) :: \phi \phi \phi (y) : \right\}|i\rangle \\
&+ \left(\frac{i\lambda_4}{4!}\right)^2\frac{1}{2!} \int d^4 x d^4 y \langle f| T\left\{ : \phi \phi \phi \phi (x) :: \phi \phi \phi \phi (y) :\right\} |i\rangle \\
&+ \left(\frac{i\lambda_3}{3!}\right)\left(\frac{i\lambda_4}{4!}\right) \int d^4 x d^4 y \langle f| T\left\{ : \phi \phi \phi \phi \phi \phi \phi (x) :\right\} |i\rangle + \mathcal{O}(\lambda_3^4, \lambda_4^4)
\end{align*}

a) My guess is that there will be two interaction vertices: $i \lambda_3$ and $i \lambda_4$ corresponding to $\phi^3$ and $\phi^4$ interaction terms (respectively) in the lagrangian. They look as follows (where I used dotted lines for mesons as convention)

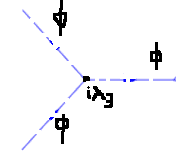
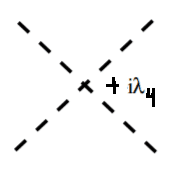
OK let's actually prove it. The idea I had in mind is to evaluate the first order terms in the expansion only, and check out explicitly that the factors of $1/3!$ and $1/4!$ cancel out.

For the first one

\begin{align*}
i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi \phi \phi (x): |i \rangle &= \frac{\lambda_3}{3!} \int d^4 x \langle f| :\left(\phi^+ + \phi^-\right)\left(\phi^+ + \phi^-\right)\left(\phi^+ + \phi^-\right)(x): |i \rangle\\
&= i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^- \phi^- (x): |i \rangle + i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^+ \phi^+ (x): |i \rangle \\
&+i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^+ \phi^+ (x): |i \rangle + i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^- \phi^- (x): |i \rangle \\
&+i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^- \phi^+ (x): |i \rangle + i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^+ \phi^- (x): |i \rangle \\
&+ i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^+ \phi^- (x): |i \rangle + i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^- \phi^+ (x): |i \rangle \\
&= i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^- (x) |i \rangle + i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^+ \phi^+ \phi^+ (x) |i \rangle \\
&+i \frac{\lambda_3}{3!} 3\int d^4 x \langle f| \phi^- \phi^+ \phi^+ (x) |i \rangle + i \frac{\lambda_3}{3!} 3\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle
\end{align*}

The issue I have in here is that when evaluating each term individually I do not get the factor of $1/3!$ canceled out. Let's show one computation explicitly

\begin{align*}
i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^- (x) |i \rangle &= i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec k}}\right)^{3/2}\langle f| b^{\dagger}(\vec k)b^{\dagger}(\vec k)b^{\dagger}(\vec k) |i\rangle \int d^4 x \exp\left(3k\cdot x\right) \\
&= i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec k}}\right)^{3/2}\langle 0| b(\vec k)b(\vec k)b(\vec k) b^{\dagger}(\vec k)b^{\dagger}(\vec k)b^{\dagger}(\vec k)|0\rangle \int d^4 x \exp\left(3k\cdot x\right) \\
&= i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec k}}\right)^{3/2}\langle 0|0\rangle \int d^4 x \exp\left(3k\cdot x\right) \\
&= i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec k}}\right)^{3/2} \frac{1}{3}\delta^{(4)}(k)
\end{align*}

Where I've used (I am indeed working in n.u.)

$$
\phi^-(x)=\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec k}} \Big)^{1/2} b^{\dagger}(\vec k)e^{ik \cdot x}
$$

$$
\big[ b (\vec k) , b^{\dagger} (\vec k') \big]=\delta_{\vec k \vec k'}
$$

$$
\int \mathrm{d}^4 x \exp(\mathrm{i} ({k}_1-{k}_2) \cdot {x})=(2 \pi)^4 \delta^{(4)}({k}_1-{k}_2).
$$
$$
\langle 0|0\rangle=1
$$

As shown, I get no $3!$ factor canceling $1/3!$ out... What am I missing? I think once I see my mistake, b) will be easier to establish

@vanhees71 , @Gaussian97 may you have time to discuss this one?

Thank you

 

[vanhees71]

First of all the vertices should read and $-\mathrm{i} \lambda_3/3!$ and $-\mathrm{i} \lambda_4/4!$ respectively.

Now to evaluate the tree-level "decay diagram" you need to give the external legs three different four-momenta and then do the calculation again.

That here the $3!$ must cancel can be seen by building the expression out of the Feynman diagrams. So you have three external points and the vertex point. At the vertex point you have three legs, each of which are indistinguishable (each standing for $\phi(x)$ in the interaction expression $\phi^3(x)$). Now you have to count the number of ways you can connect the external points (i.e., doing the contractions of the external points with the vertex point in the sense of Wick's theorem): For the first external point you have 3 choices of legs, for the 2nd external point you have 2 choices of legs and for the final external point there's only 1 leg left. All the choices give the same, i.e., the factor you have to multiply the expression with is $3 \cdot 2 \cdot 1=3!$, which cancels the $3!$. So the Feynman rule in position space gives $(-\mathrm{i} \lambda_3/3! \cdot 3! \mathrm{i} G(x-x_1) \mathrm{i} G(x-x_2) \mathrm{i} G(x-x_3)$. With the Fourier transform to momentum space you get an energy-momentum conserving factor $(2 \pi) \delta^{(4)}(p_1+p_2+p_3)$ and the Green's functions transform to $G(p_1)$, $G(p_2)$, and $G(p_3)$.

To get this using the analytic expressions is a pretty tedious task even for this simple tree-level diagram. The message of the exercise is, how amazingly efficient are Feynman's rules which are just ingeneous mathematical notations for the expressions occurring in the perturbation series for S-matrix elements.

 

[JD_PM]

Thank you very much @vanhees71

Now to evaluate the tree-level "decay diagram" you need to give the external legs three different four-momenta and then do the calculation again.

Mmm I think I understand. Now I get (I actually noticed I completely forgot about the $(2\pi)^4$ factor one picks up due to the Fourier transform)

$$
i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^- (x) |i \rangle =
i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} (2\pi)^4 \delta^{(4)}(p_1+p_2+p_3)
$$

Mmm but I still do not pick up the 3! factor out if this computation...

That here the $3!$ must cancel can be seen by building the expression out of the Feynman diagrams. So you have three external points and the vertex point. At the vertex point you have three legs, each of which are indistinguishable (each standing for $\phi(x)$ in the interaction expression $\phi^3(x)$). Now you have to count the number of ways you can connect the external points (i.e., doing the contractions of the external points with the vertex point in the sense of Wick's theorem): For the first external point you have 3 choices of legs, for the 2nd external point you have 2 choices of legs and for the final external point there's only 1 leg left. All the choices give the same, i.e., the factor you have to multiply the expression with is $3 \cdot 2 \cdot 1=3!$, which cancels the $3!$. So the Feynman rule in position space gives $(-\mathrm{i} \lambda_3/3! \cdot 3! \mathrm{i} G(x-x_1) \mathrm{i} G(x-x_2) \mathrm{i} G(x-x_3)$. With the Fourier transform to momentum space you get an energy-momentum conserving factor $(2 \pi) \delta^{(4)}(p_1+p_2+p_3)$ and the Green's functions transform to $G(p_1)$, $G(p_2)$, and $G(p_3)$.

Really clear explanation, thank you.

At the vertex point you have three legs, each of which are indistinguishable (each standing for $\phi(x)$ in the interaction expression $\phi^3(x)$). Now you have to count the number of ways you can connect the external points (i.e., doing the contractions of the external points with the vertex point in the sense of Wick's theorem): For the first external point you have 3 choices of legs, for the 2nd external point you have 2 choices of legs and for the final external point there's only 1 leg left.

Oh that is really interesting! Please let me check if I understand correctly; based on Wick's theorem we get (where underbrace denotes contraction)

\begin{align*}
&T\{:\phi \phi \phi(x)::\phi \phi \phi(y):\} = \ :\phi \phi \phi(x) \phi \phi \phi(y): \\
&+:\phi \phi \underbrace{\phi(x) \phi} \phi \phi(y): + :\phi \underbrace{\phi \phi(x) \phi \phi} \phi(y): + :\underbrace{\phi \phi \phi(x) \phi \phi \phi(y)}: \\
&+:\underbrace{\phi \phi \underbrace{\phi(x) \phi} \phi \phi(y)}: + :\phi \underbrace{\phi \underbrace{\phi(x) \phi} \phi} \phi(y): + :\underbrace{\phi \underbrace{\phi \phi(x) \phi \phi} \phi(y)}: \\
&+:\underbrace{\phi \underbrace{\phi \underbrace{\phi(x) \phi} \phi} \phi(y)}: \\
&= \ :\phi \phi \phi(x) \phi \phi \phi(y): + 3\Delta_F (x-y):\phi \phi (x) \phi \phi (y): + 3\left(\Delta_F (x-y)\right)^2 :\phi (x) \phi (y): + \left(\Delta_F (x-y)\right)^3
\end{align*}

At the beginning we have 3 possible choices: either $:\phi \phi \underbrace{\phi(x) \phi} \phi \phi(y):, :\phi \underbrace{\phi \phi(x) \phi \phi} \phi(y):$ or $:\underbrace{\phi \phi \phi(x) \phi \phi \phi(y)}:$. Let's say we choose $:\phi \phi \underbrace{\phi(x) \phi} \phi \phi(y):$. Then we have two possible choices for the second external point; either $:\underbrace{\phi \phi \underbrace{\phi(x) \phi} \phi \phi(y)}:$ or $:\phi \underbrace{\phi \underbrace{\phi(x) \phi} \phi} \phi(y):$. Let's say we choose $:\underbrace{\phi \phi \underbrace{\phi(x) \phi} \phi \phi(y)}:$. Then the only possible choice for the final external point is $:\underbrace{\phi \underbrace{\phi \underbrace{\phi(x) \phi} \phi} \phi(y)}:$.

To get this using the analytic expressions is a pretty tedious task even for this simple tree-level diagram. The message of the exercise is, how amazingly efficient are Feynman's rules which are just ingeneous mathematical notations for the expressions occurring in the perturbation series for S-matrix elements.

I totally agree that in practice it has to be much better to start off writing the Feynman diagram, just using it as a 'mnemonic device'.

But given that I am a beginner, would not be useful to do the tedious calculation at least once?

 

[Gaussian97]

Well, first of all, let's agree on what is exactly the Feynman rule for the vertex. Using the Feynman rules for diagrams, it's easy to see that, in this case, the Feynman rule for a $3\phi$ vertex is just the amplitude of a process involving 3 "particles" $\phi$ at tree-level. So let's choose a fixed amplitude to compute (the result is independent on what we choose).

I agree that it is really instructive to do this tedious calculation at least one in your life, so I propose to compute the amplitude for the $\phi \to \phi + \phi$ process at first order in perturbation series.
So in this case what should be the initial state $\left|\phi\right>$ and final state $\left|\phi\phi\right>$? (Let's call $p_1, p_2, p_3$ to the three momenta of those particles).
Now, the S-matrix expansion is
$$S = \langle \phi\phi | \phi \rangle + i \frac{\lambda_3}{3!} \int d^4 x \langle \phi\phi| :\phi(x) \phi(x) \phi (x): |\phi\rangle + i\frac{\lambda_4}{4!} \int d^4 x \langle \phi\phi | :\phi(x) \phi(x) \phi(x) \phi (x) : | \phi \rangle $$
Now show that the first and last terms vanish and then, from all the terms arising from splitting $\phi = \phi^+ + \phi^-$ look which ones survive.

 

[JD_PM]

Hi @Gaussian97!

So you propose the unphysical process $\phi \to \phi + \phi$

We have as initial and final states

$$|i\rangle = b^{\dagger}(\vec p_1) |0\rangle$$

$$|f\rangle = b^{\dagger}(\vec p_2)b^{\dagger}(\vec p_3) |0\rangle$$

Incidentally, I think we missed a -ive sign coming from Dyson's formula (we have the factor $(-i)^n/n!$; as we are in first order we indeed get $-i$)

The S-matrix reads (please let me use f, i instead ;))

$$S = \langle f | i \rangle - i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi(x) \phi(x) \phi (x): |i\rangle - i\frac{\lambda_4}{4!} \int d^4 x \langle f| :\phi(x) \phi(x) \phi(x) \phi (x) : | i \rangle$$


Let's go slowly. For $\langle f | i \rangle$ I get

\begin{equation*}
\langle f | i \rangle = \langle 0 | b(\vec p_2)b(\vec p_3) b^{\dagger} (\vec p_1) |0\rangle=\langle 0 | b(\vec p_2)[b(\vec p_3),b^{\dagger} (\vec p_1)] |0\rangle=\langle 0 | b(\vec p_2) |0\rangle = 0
\end{equation*}

Where I've used the fact that $b(\vec p_2) |0\rangle=0$. So as you said, the non-scattering term vanishes.

Computing $- i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi(x) \phi(x) \phi (x): |i\rangle$ ...

 

[Gaussian97]

Ok

$$|i\rangle = b^{\dagger}(\vec p_1) |0\rangle$$

$$|f\rangle = b^{\dagger}(\vec p_2)b^{\dagger}(\vec p_3) |0\rangle$$

Perfect, that was just to join notation with the normalization factor (which is not really important now)

Let's go slowly. For $\langle f | i \rangle$ I get

\begin{equation*}
\langle f | i \rangle = \langle 0 | b(\vec p_2)b(\vec p_3) b^{\dagger} (\vec p_1) |0\rangle=\langle 0 | b(\vec p_2)[b(\vec p_3),b^{\dagger} (\vec p_1)] |0\rangle=\langle 0 | b(\vec p_2) |0\rangle = 0
\end{equation*}

Where I've used the fact that $b(\vec p_2) |0\rangle=0$. So as you said, the non-scattering term vanishes.

Ok, to be 100% clear, should be
$$\langle f | i \rangle = \langle 0 | b(\vec p_2)[b(\vec p_3),b^{\dagger} (\vec p_1)] |0\rangle=\delta^{(3)}(\vec{p}_3 - \vec{p}_1)\langle 0 | b(\vec p_2) |0\rangle = 0$$

 

[JD_PM]

Computing $- i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi(x) \phi(x) \phi (x): |i\rangle$ ...

Let's compute it in detail

\begin{align*}

-i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi \phi \phi (x): |i \rangle &= -i\frac{\lambda_3}{3!} \int d^4 x \langle f| :\left(\phi^+ + \phi^-\right)\left(\phi^+ + \phi^-\right)\left(\phi^+ + \phi^-\right)(x): |i \rangle\\

&= -i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^- \phi^- (x): |i \rangle - i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^+ \phi^+ (x): |i \rangle \\

&-i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^+ \phi^+ (x): |i \rangle - i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^- \phi^- (x): |i \rangle \\

&-i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^- \phi^+ (x): |i \rangle - i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^+ \phi^- (x): |i \rangle \\

&- i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^- \phi^+ \phi^- (x): |i \rangle - i \frac{\lambda_3}{3!}\int d^4 x \langle f| : \phi^+ \phi^- \phi^+ (x): |i \rangle \\

&= -i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^- (x) |i \rangle - i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^+ \phi^+ \phi^+ (x) |i \rangle \\

&-i \frac{\lambda_3}{3!} 3\int d^4 x \langle f| \phi^- \phi^+ \phi^+ (x) |i \rangle - i \frac{\lambda_3}{3!} 3\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle

\end{align*}

The above yields all tree diagrams associated to our theory; we are only interested in $\phi \to \phi + \phi$ though, so we focus on the last term to get

\begin{align*}
&-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle = \\
&=-3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \times \\
&\times \langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec p_2) b^{\dagger}(\vec p_3)b(\vec p_1)b^{\dagger}(\vec p_1)|0\rangle \int d^4 x \exp\left(-ix\cdot(p_1-p_2-p_3)\right) \\
&=-3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \times \\
&\times \langle 0| b(\vec p_2)[b(\vec p_3),b^{\dagger}(\vec p_2)] b^{\dagger}(\vec p_3)[b(\vec p_1),b^{\dagger}(\vec p_1)]|0\rangle \int d^4 x \exp\left(-ix\cdot(p_1-p_2-p_3)\right) \\
&= -3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \times \\
&\times \langle 0| [b(\vec p_2), b^{\dagger}(\vec p_3)]|0\rangle \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p_2-p_3\right) \\
&= -3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p_2-p_3\right)
\end{align*}

So we conclude that

\begin{align*}
&-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle = \\
&= -3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p_2-p_3\right)
\end{align*}

Do you agree so far?

 

[Gaussian97]

Nop, not really.

The above yields all tree diagrams associated to our theory; we are only interested in $\phi \to \phi + \phi$ though, so we focus on the last term

well, maybe this is too obvious for you, but I must ask to be sure, why do you focus only on the last term? What happens to all the other terms?

\begin{align*}
&-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle = \\
&=-3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \times \\
&\times \langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec p_2) b^{\dagger}(\vec p_3)b(\vec p_1)b^{\dagger}(\vec p_1)|0\rangle \int d^4 x \exp\left(-ix\cdot(p_1-p_2-p_3)\right) \\
\end{align*}

I don't agree with that, could you please expand $\phi^{\pm}(x)$ in terms of creation and anihilation operators?

 

[JD_PM]

well, maybe this is too obvious for you, but I must ask to be sure, why do you focus only on the last term? What happens to all the other terms?

Thank you for asking. This is what I think . We recall what the initial and final states are

$$|i\rangle = b^{\dagger}(\vec p_1) |0\rangle$$

$$|f\rangle = b^{\dagger}(\vec p_2)b^{\dagger}(\vec p_3) |0\rangle$$

This means that the only matrix element which will not vanish will be the one having 2 creation operators and 1 anihilation operator; the only matrix element fitting this condition is the one I computed. What happens to the rest?

1. The one containing 3 creation operators will vanish, because there are only two annihilation operators in $\langle f|$ and the remaining creation operator will hit $\langle 0|$.
2. The one containing 3 annihilation operators will vanish, because there is only one creation operator in $|f\rangle$ and any of the remaining 2 annihilation operators will hit $|0\rangle$.
3. The one containing 2 annihilation operators and 1 creation operator will vanish, because there is only one creation operator in $|f\rangle$ and the remaining annihilation operator will hit $|0\rangle$.

Nop, not really.

Looking at your comment on why I computed it incorrectly...

 

[Gaussian97]

Thank you for asking. This is what I think . We recall what the initial and final states are

$$|i\rangle = b^{\dagger}(\vec p_1) |0\rangle$$

$$|f\rangle = b^{\dagger}(\vec p_2)b^{\dagger}(\vec p_3) |0\rangle$$

This means that the only matrix element which will not vanish will be the one having 2 creation operators and 1 anihilation operator; the only matrix element fitting this condition is the one I computed. What happens to the rest?

1. The one containing 3 creation operators will vanish, because there are only two annihilation operators in $\langle f|$ and the remaining creation operator will hit $\langle 0|$.
2. The one containing 3 annihilation operators will vanish, because there is only one creation operator in $|f\rangle$ and any of the remaining 2 annihilation operators will hit $|0\rangle$.
3. The one containing 2 annihilation operators and 1 creation operator will vanish, because there is only one creation operator in $|f\rangle$ and the remaining annihilation operator will hit $|0\rangle$.

Okay perfect, it was just to check that we are not really "focusing" on the last term, we are focusing on all the terms, just happen that all the others are 0, you can use a similar argument to show that all the terms in the $\phi^4$ term also vanish, which maybe would be a good idea to do before continuing studying the $\phi^3$ terms.

Looking at your comment on why I computed it incorrectly...

Well, just write $\phi^{(\pm)}(x)$ in terms of creation and annihilation operators and substitute into
$$-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^-(x) \phi^-(x) \phi^+ (x) |i \rangle$$
and you'll find that the expression is not the one you have. To clarify exactly the problems I need to see how you write $\phi^{(\pm)}(x)$, to see the conventions you use.

 

[JD_PM]

Well, just write $\phi^{(\pm)}(x)$ in terms of creation and annihilation operators and substitute into
$$-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^-(x) \phi^-(x) \phi^+ (x) |i \rangle$$
and you'll find that the expression is not the one you have. To clarify exactly the problems I need to see how you write $\phi^{(\pm)}(x)$, to see the conventions you use.

$$-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^-(x) \phi^-(x) \phi^+ (x) |i \rangle=$$

$$=-3 i \frac{\lambda_3}{3!} K \int d^4 x \langle f|b^{\dagger} (\vec p_2)b^{\dagger} (\vec p_3)b (\vec p_1)|i \rangle e^{-ix \cdot (p_1 -p_2 -p_3)} $$

I have checked my previous computation and (please correct me if I am wrong) the only mistake I see is that I did not normal-order correctly. However, the result I get is exactly the same.

 

[Gaussian97]

Sorry, but no, please, what expression are you using for $\phi^{(\pm)}(x)$?

 

[JD_PM]

Sorry, but no, please, what expression are you using for $\phi^{(\pm)}(x)$?

$$\phi^-(x)=\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} b^{\dagger}(\vec p)e^{ip\cdot x}$$

$$\phi^+(x)=\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} b(\vec p)e^{-ip \cdot x}$$

 

[Gaussian97]

Okay, I'm not used doing these things in the discrete case, and I'm not even sure if it's okay, are you following some book? In any case, this explains some differences between us.
But still, that doesn't explain the equations you wrote before, using these equations you have shown me there, can you compute
$\phi^{-}(x) \phi^+(x)$?
And $\phi^{-}(x) \phi^{-}(x) \phi^+(x)$

 

[JD_PM]

Okay, I'm not used doing these things in the discrete case, and I'm not even sure if it's okay, are you following some book? In any case, this explains some differences between us.

Oops my bad! I was only dealing with the creation and destruction of one type of particle. Instead, I should be dealing with two types. The following may look better

$$\phi(x) = \phi^+ (x) + \phi^- (x) =
\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} \left(a(\vec p)e^{-ip\cdot x}+b^{\dagger}(\vec p)e^{ip\cdot x}\right)$$


I follow Mandl & Shaw (page 44)

 

[JD_PM]

Oops my bad! I was only dealing with the creation and destruction of one type of particle. Instead, I should be dealing with two types. The following may look better

$$\phi(x) = \phi^+ (x) + \phi^- (x) =
\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} \left(a(\vec p)e^{-ip\cdot x}+b^{\dagger}(\vec p)e^{ip\cdot x}\right)$$


I follow Mandl & Shaw (page 44)

I've been thinking a bit about this. If we assume two types of particles then we would need another expansion, involving $\phi^{\dagger}$.

I think we should only working with the destruction/creation of only one type of particle. I believe you wanted to use the following expansion though

 

[Gaussian97]

Well, as you say, we should only work with one type of particle, because using the condition $\mathscr{L}=\mathscr{L}^\dagger$ we obtain that $\phi = \phi^\dagger$, so $a(\vec{p})=b(\vec{p})$

And yes, I'm more comfortable using the continuous expansion of $\phi$, but if you are supposed to do it with the discrete case, let's do it. In any case, continuum or discrete, can you give an expression for
$$\phi^-(x)\phi^+(x)$$?

 

[JD_PM]

Yes, in class we worked with discrete mode expansions so let us please do the same in here. Just to be clear before performing the computation; we will use the following mode expansion

$$\phi(x) = \phi^+ (x) + \phi^- (x) = \sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} \left(b(\vec p)e^{-ip\cdot x}+b^{\dagger}(\vec p)e^{ip\cdot x}\right)$$

Where

$$\phi^-(x)=\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} b^{\dagger}(\vec p)e^{ip\cdot x}$$

$$\phi^+(x)=\sum_{\vec k} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} b(\vec p)e^{-ip\cdot x}$$

i.e. we only deal with the creation and annihilation of the b particle.

Do you agree?

 

[Gaussian97]

Yes, I agree, and to be clear, $\vec{p}=\vec{k}$, right?

 

[JD_PM]

Yes, I agree, and to be clear, $\vec{p}=\vec{k}$, right?

Yes.

So we get

$$\phi^-(x)\phi^+(x)=$$

$$=\sum_{\vec p} \sum_{\vec p'} \Big(\frac{1}{2V \omega_{\vec p}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec p'}} \Big)^{1/2} b^{\dagger} (\vec p) b (\vec p') e^{-ix\cdot (p'-p)}$$


Where I labeled the momentum of the created particle to be $\vec p$ and the momentum of the annihilated particle to be $\vec p'$

 

[Gaussian97]

Ok, perfect, now can you do the same for
$$\phi^-(x)\phi^-(x)\phi^+(x)$$?

 

[JD_PM]

Yes.

Let us label the momentum of the two created b particles to be $\vec p_2$ and $\vec p_3$ and the momentum of the annihilated b particle to be $\vec p_1$ (just as I originally did). Then we get

$$\phi^-(x)\phi^-(x)\phi^+(x)= $$

$$=\sum_{\vec p_2} \sum_{\vec p_3} \sum_{\vec p_1} \Big(\frac{1}{2V \omega_{\vec p_2}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec p_3}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec p_1}} \Big)^{1/2} b^{\dagger} (\vec p_2) b^{\dagger} (\vec p_3) b (\vec p_1) e^{-ix\cdot (p_1-p_2 -p_3)}$$

 

[Gaussian97]

Well, the expression is correct, but I think we should clarify some concepts here.
First of all, we talk about creation and annihilation operators because it's the conventional names to $b$ and $b^\dagger$, but we are not creating nor annihilating anything now.
We are no longer studying the $\phi \to 2\phi$ process we started with, we are only computing the quantity
$$\phi^{-2}(x)\phi^+(x)$$
which of course, in the same way as $\phi(x)$, has well-defined expresion in terms of $b$ and $b^\dagger$ indepenent on what process we study.
So, no, $p_i$ are not any momenta of any created or annihilated particles (because we are not creating anything), they are just dummy labels with no physical meaning.

Now of course, even if the expression is correct, you shouldn't use the labels $p_1, p_2, p_3$ because we want to use them to label the physical momenta of our problem. If you prefer to use this expression we should change the notation we establish in #4 and #5.

 

[JD_PM]

Alright, I see.

Now that it is more clear, should I post my second attempt of the computation of $-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^-(x) \phi^-(x) \phi^+ (x) |i \rangle$ or do you want to add something else first?

 

[Gaussian97]

Well, now that you have the expression for $\phi^{-2}(x)\phi^+(x)$ you can try again with the computation of the vertex.
In any case, I would write again in the next post the expressions of the initial and final states, and the complete expression for $\phi^{-2}(x)\phi^+(x)$.
Then you can simply substitute to the equation
$$- i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi(x) \phi(x) \phi (x): |i\rangle$$

Remember that the expressions you give in post #9 and #22 are correct but notational incompatible with each other.

 

[JD_PM]

Alright, let's proceed.

In any case, I would write again in the next post the expressions of the initial and final states, and the complete expression for $\phi^{-2}(x)\phi^+(x)$.
...
Remember that the expressions you give in post #9 and #22 are correct but notational incompatible with each other.

Oh I see what you meant.

So let us write the general formulae using $\vec k_1, \vec k_2, \vec k_3$ as dummy indices (where $\vec k_1, \vec k_2, \vec k_3$ have no physical meaning here).

$$|i\rangle = b^{\dagger}(\vec k_1) |0\rangle$$

$$|f\rangle = b^{\dagger}(\vec k_2)b^{\dagger}(\vec k_3) |0\rangle$$

We also have

$$\phi^-(x)\phi^-(x)\phi^+(x)=$$

$$=\sum_{\vec k_2} \sum_{\vec k_3} \sum_{\vec k_1} \Big(\frac{1}{2V \omega_{\vec k_2}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec k_3}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec k_1}} \Big)^{1/2} b^{\dagger} (\vec k_2) b^{\dagger} (\vec k_3) b (\vec k_1) e^{-ix\cdot (k_1-k_2 -k_3)}$$

Next I will compute

$$- i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi(x) \phi(x) \phi (x): |i\rangle$$

Just to be clear: I will use $\vec p$ notation because such term represents the $\phi \to \phi \phi$ process.

 

[Gaussian97]

So let us write the general formulae using $\vec k_1, \vec k_2, \vec k_3$ as dummy indices (where $\vec k_1, \vec k_2, \vec k_3$ have no physical meaning here).

$$|i\rangle = b^{\dagger}(\vec k_1) |0\rangle$$

$$|f\rangle = b^{\dagger}(\vec k_2)b^{\dagger}(\vec k_3) |0\rangle$$

Well, again, you can use the label you want for the momenta of the particles, but now $\vec{k}_i$ are not dummy indices and they do have physical meaning. $b^{\dagger}(\vec k_1) |0\rangle$ describes a particle of type '$b$' with momentum $k_1$, which of course is physical.

We also have

$$\phi^-(x)\phi^-(x)\phi^+(x)=$$

$$=\sum_{\vec k_2} \sum_{\vec k_3} \sum_{\vec k_1} \Big(\frac{1}{2V \omega_{\vec k_2}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec k_3}} \Big)^{1/2} \Big(\frac{1}{2V \omega_{\vec k_1}} \Big)^{1/2} b^{\dagger} (\vec k_2) b^{\dagger} (\vec k_3) b (\vec k_1) e^{-ix\cdot (k_1-k_2 -k_3)}$$

Now you are using the same label that you use to describe the physical momenta of the particles to describe also the dummy labels that appear in the expression of $\phi^{-2}(x)\phi^+(x)$. Again all your equation here are correct, and if you want you can proceed to substitute into the amplitude, but the equations as you have them now are still notation incompatible.

 

[JD_PM]

Well, again, you can use the label you want for the momenta of the particles, but now $\vec{k}_i$ are not dummy indices and they do have physical meaning. $b^{\dagger}(\vec k_1) |0\rangle$ describes a particle of type '$b$' with momentum $k_1$, which of course is physical.


Now you are using the same label that you use to describe the physical momenta of the particles to describe also the dummy labels that appear in the expression of $\phi^{-2}(x)\phi^+(x)$. Again all your equation here are correct, and if you want you can proceed to substitute into the amplitude, but the equations as you have them now are still notation incompatible.

Yikes, then I do not understand what you mean with notation here. But, if you wish, let's postpone this discussion for later and focus on the computation

 

[JD_PM]

I will include as much detail as possible

\begin{align*}
&-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle = \\
&=-3i \frac{\lambda_3}{3!}\sum_{\vec p'_2}\sum_{\vec p'_3}\sum_{\vec p'_1}\left(\frac{1}{2V \omega_{\vec p'_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p'_3}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p'_1}}\right)^{1/2} \times \\
&\times \langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec p'_2) b^{\dagger}(\vec p'_3)b(\vec p'_1)b^{\dagger}(\vec p_1)|0\rangle \int d^4 x \exp\left(-ix\cdot(p'_1-p'_2-p'_3)\right) \\
&=-3i \frac{\lambda_3}{3!}\sum_{\vec p'_2}\sum_{\vec p'_3}\sum_{\vec p'_1}\left(\frac{1}{2V \omega_{\vec p'_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p'_3}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p'_1}}\right)^{1/2} \times \\
&\times \langle 0| b(\vec p_2)[b(\vec p_3),b^{\dagger}(\vec p'_3)] b^{\dagger}(\vec p'_2)[b(\vec p'_1),b^{\dagger}(\vec p_1)]|0\rangle \int d^4 x \exp\left(-ix\cdot(p'_1-p'_2-p'_3)\right) \\
&= -3i \frac{\lambda_3}{3!}\sum_{\vec p'_2}\left(\frac{1}{2V \omega_{\vec p'_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2} \times \\
&\times \langle 0| [b(\vec p_2), b^{\dagger}(\vec p'_2)]|0\rangle \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p'_2-p_3\right) \\
&= -3i \frac{\lambda_3}{3!}\left(\frac{1}{2V \omega_{\vec p_1}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec p_3}}\right)^{1/2} \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p_2-p_3\right) \\
&= -\frac{3}{2}i \frac{\lambda_3}{3!}\left(\frac{1}{2V^3 \omega_{\vec p_1}\omega_{\vec p_2}\omega_{\vec p_3}}\right)^{1/2} \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p_2-p_3\right)
\end{align*}

Where I have used the following commutation relations (because mesons obey Bose-Einstein statistics)

\begin{equation*}
[b(\vec p), b^{\dagger}(\vec p')]=\delta_{\vec p, p'}
\end{equation*}

\begin{equation*}
[b^{\dagger}(\vec p), b^{\dagger}(\vec p')]=0=[b(\vec p), b(\vec p')]
\end{equation*}

And the fact that (I just pick the following as an example; it works the same way for the rest of primed terms)

\begin{equation*}
\sum_{\vec p'_2} \delta_{\vec p'_2, \vec p_2}\left(\frac{1}{2V \omega_{\vec p'_2}}\right)^{1/2} = \left(\frac{1}{2V \omega_{\vec p_2}}\right)^{1/2}
\end{equation*}

So we conclude that

\begin{align*}
&-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle = \\
&= -\frac{3}{2}i \frac{\lambda_3}{3!}\left(\frac{1}{2V^3 \omega_{\vec p_1}\omega_{\vec p_2}\omega_{\vec p_3}}\right)^{1/2} \left( 2 \pi \right)^4 \delta^{(4)}\left(p_1-p_2-p_3\right)
\end{align*}

Notice that I get the exact same answer than before...

 

[Gaussian97]

Yikes, then I do not understand what you mean with notation here. But, if you wish, let's postpone this discussion for later and focus on the computation

You cannot do the computation without understanding this. You are using the same name for two different things, so any computation from here will be inevitably wrong. So answer my question, what is the relation between the $\vec{k}_1$ appearing in
$$\left|i\right>=b^\dagger(\vec{k}_1)\left|0\right>$$
and the $\vec{k}_1$ appearing in the $\phi^{-2}(x)\phi^{+}(x)$ expression?

 

[JD_PM]

Mmm

This is what I understand

$$\left|i\right>=b^\dagger(\vec{k}_1)\left|0\right>$$

Here $\vec k_1$ stands for the momentum of the incoming b particle before the process occurs

While here

$$\phi^-(x)\phi^-(x)\phi^{+}(x) \sim b(\vec k_1)$$

Stands for the momentum of the incoming b particle after the process occurs.

But I am not sure of this. Could please shed some light?

 

[Gaussian97]

Okay, $b^\dagger$ is called the creation operator because when one applies this operator to the ground state $\left|0\right>$ it describes a one-particle state (so, this operator takes a state with no particles and returns a state with one particle, it "creates" a particle).
The operator $b^\dagger$ is not unique, there are infinite "creation operators" that will create different states, in our case the operator $b^\dagger$ is completely specified by a vector, let's call it $\vec{v}$. So given a vector $\vec{v}$ we can contruct a creation operator $b^\dagger(\vec{v})$ that will create a certain one-particle state when acting on the vacuum (the groud state).
Furthermore one can see that this one-particle state is an eigenstate of the Momentum operator ($\hat{\vec{P}}$) with eigenvalue $\vec{v}$, that's the reason we say that $b^\dagger(\vec{p})$ creates a particle with momentum $\vec{p}$.
Therefore when you write something like
$$\left|i\right> = b^\dagger(\vec{p}) \left|0\right>$$
You say that the $\left|i\right>$ state describes a single-particle state and that the particle has 3-momentum $\vec{p}$ (i.e. it is eigenstate of $\hat{\vec{P}}$).

Outside that, if $b^\dagger(\vec{v})$ doesn't act on a physical state, $\vec{v}$ it's nothing more than a label, a way to differentiate different operators, with no relation with momentum or any physical property.
So, when you write the expression for $\phi^{-2}(x)\phi^+(x)$, this is just another operator, that you can relate to the creation and annihilation operators because there's a mathematical relation, but when you have the operator
$$\sum_{\vec k_2} \sum_{\vec k_3} \sum_{\vec k_1} b^{\dagger} (\vec k_2) b^{\dagger} (\vec k_3) b (\vec k_1) e^{-ix\cdot (k_1-k_2 -k_3)}$$
the labels $k_1, k_2, k_3$ mean nothing, are dummy indices that you use to sum over all the operators, in the same way that, in the expression
$$\sum_{n=0}^{\infty} \frac{1}{2^n}$$
$n$ is meaningless.
So you cannot use $k_1, k_2, k_3$ to denote both, the physical momenta of the particles in your initial and final state and, simultaneously, the dummy indices appearing to write the operator $\phi^{-2}(x)\phi^+(x)$, in the same way as you cannot use $k_1$ to describe all three momenta of the particles, or you cannot use $k_1$ for all three momenta appearing in $\phi^{-2}(x)\phi^+(x)$ and write the operator as
$$\sum_{\vec k_1} b^{\dagger} (\vec k_1) b^{\dagger} (\vec k_1) b (\vec k_1) e^{ix\cdot k_1}$$
If you do any of these things, you are using the same label for different things, and therefore you will make mistakes.

 

[JD_PM]

Thank you very much for you explanation.

Fortunately I corrected the mistake in my last attempt (#29)

I will include as much detail as possible

\begin{align*}
&-3 i \frac{\lambda_3}{3!}\int d^4 x \langle f| \phi^- \phi^- \phi^+ (x) |i \rangle = \\
&=-... \\
&\times \langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec p'_2) b^{\dagger}(\vec p'_3)b(\vec p'_1)b^{\dagger}(\vec p_1)|0\rangle ... \\
&=...
\end{align*}

Notice that I labeled the momentum vectors in the initial and final states unprimed, while the momentum vectors associated to the sandwiched $\phi^{\pm}$ are primed. So I am confident that if there is a mistake in the mistake #29, it is not related to the labeling of momenta.

Do you see any mistake in #29 though?

 

[Gaussian97]

Oh, with all the daggers and arrows I completely missed the primes, then I'm sorry. You're right. Let's look at your computation step by step, let me rewrite your primed as $\vec{k}$ if you don't care, I think is much more visual.
$$
\begin{align*}

&-3i \frac{\lambda_3}{3!}\sum_{\vec k_2}\sum_{\vec k_3}\sum_{\vec k_1}\left(\frac{1}{2V \omega_{\vec k_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec k_3}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec k_1}}\right)^{1/2} \times \\

&\times \langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec k_2) b^{\dagger}(\vec k_3)b(\vec k_1)b^{\dagger}(\vec p_1)|0\rangle \int d^4 x \exp\left(-ix\cdot(k_1-k_2-k_3)\right) \\

&=-3i \frac{\lambda_3}{3!}\sum_{\vec k_2}\sum_{\vec k_3}\sum_{\vec k_1}\left(\frac{1}{2V \omega_{\vec k_2}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec k_3}}\right)^{1/2}\left(\frac{1}{2V \omega_{\vec k_1}}\right)^{1/2} \times \\

&\times \langle 0| b(\vec p_2)[b(\vec p_3),b^{\dagger}(\vec k_3)] b^{\dagger}(\vec k_2)[b(\vec k_1),b^{\dagger}(\vec p_1)]|0\rangle \int d^4 x \exp\left(-ix\cdot(k_1-k_2-k_3)\right) \\
\end{align*}
$$
I agree that
$$\langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec k_2) b^{\dagger}(\vec k_3)b(\vec k_1)b^{\dagger}(\vec p_1)|0\rangle = \langle 0| b(\vec p_2)b(\vec p_3)b^{\dagger}(\vec k_3) b^{\dagger}(\vec k_2)[b(\vec k_1),b^{\dagger}(\vec p_1)]|0\rangle$$
But I don't see how you get the commutator between $p_3$ and $k_3$ terms

 

[JD_PM]

Oh, with all the daggers and arrows I completely missed the primes, then I'm sorry. You're right. Let's look at your computation step by step, let me rewrite your primed as $\vec{k}$ if you don't care, I think is much more visual.

No problem.

But I don't see how you get the commutator between $p_3$ and $k_3$ terms

Notice that mesons are bosons so they obey Bose-Einstein statistics, which means that we should impose commutation relations i.e.

\begin{equation*}

[b(\vec p), b^{\dagger}(\vec k)]=\delta_{\vec p, \vec k}

\end{equation*}

\begin{equation*}

[b^{\dagger}(\vec p), b^{\dagger}(\vec k)]=0=[b(\vec p), b(\vec k)]

\end{equation*}

Do you agree so far?