Lubrication theory for two spheres -- Finding the resisting force

[JyJ]

Homework Statement

Show that the force resisting change of the minimum distance h between the surfaces of two rigid spheres of radii a and b which are nearly touching is:
$$6\pi\frac{\mu}{h({a^{-1} + b^{-1}})^2}\frac{dh}{dt}$$
provided
$$\frac{\rho h}{\mu}\frac{dh}{dt}$$

Homework Equations

Reynolds lubrication equation:
$$(h^3p_x)_x +(h^3p_y)_y = 6\mu(h(U_x+V_y) - (Uh_x+Vh_y)+2W)$$
where U(x,y,t), V(x,y,t) and W(x,y,t) describe the motion of the surface

The Attempt at a Solution

I suppose we can say that $$W=\dot{h}$$ and $$U=V=0$$ Since h is uniform in x and y, the Reynolds lubrication equation may be simplified to:
$$h^3{\nabla}^2p = 12\mu \dot{h}$$
Assuming symmetry around θ:
$$p_{rr}+\frac{1}{r}p_r = 12\mu \frac{dh}{dt}\frac{1}{h^3}$$
$$ p = \frac{3\mu \dot{h}r^2}{h^3} + A $$
Assume on r = a, p = p_a:
$$ p = p_a + \frac{3\mu \dot{h}}{h^3}(r^2 - a^2)$$
The total upward force is:
$$2\pi\int{p-p_a}rdr$$
But in here I am struggling to put up the limits for the integral as because we have two spheres nearly touching, r would vary similarly as it would vary between two parabolas.

 

[Chestermiller]

A simpler version of this problem is pressing two flat circular plates together. Have you solved that problem first?

 

[JyJ]

A simpler version of this problem is pressing two flat circular plates together. Have you solved that problem first?

I solved a similar problem with a rigid plane and a circular disk of radius a. I followed the same procedure but for the limits of the integral it was easier to find them and they were just from 0 to a. However, here I am struggling to find the limits.

 

[Chestermiller]

I solved a similar problem with a rigid plane and a circular disk of radius a. I followed the same procedure but for the limits of the integral it was easier to find them and they were just from 0 to a. However, here I am struggling to find the limits.

I can help you. Let the axis of the system be the line joining the centers of the two spheres, and extend to infinity in both directions. Let r be the radial distance from this axis. For values of r that are small compared to the radii of the two spheres, show that the gap between the spheres is approximately $$H=h+\left(\frac{1}{a}-\frac{1}{b}\right)\frac{r^2}{2}$$where a is the radius of the smaller sphere. Then show that the volume of fluid in this gap out to radius r is $$V=\pi r^2\left[h+\left(\frac{1}{a}-\frac{1}{b}\right)\frac{r^2}{4}\right]$$From this relationship, what is the rate of change of this volume with respect to time?

 

[JyJ]

I can help you. Let the axis of the system be the line joining the centers of the two spheres, and extend to infinity in both directions. Let r be the radial distance from this axis. For values of r that are small compared to the radii of the two spheres, show that the gap between the spheres is approximately $$H=h+\left(\frac{1}{a}-\frac{1}{b}\right)\frac{r^2}{2}$$where a is the radius of the smaller sphere. Then show that the volume of fluid in this gap out to radius r is $$V=\pi r^2\left[h+\left(\frac{1}{a}-\frac{1}{b}\right)\frac{r^2}{4}\right]$$From this relationship, what is the rate of change of this volume with respect to time?

Thanks for your reply. Could you please hint me on how the first approximation for H can be achieved. I suppose since you mentioned for r small compared to the radii of the spheres, Taylor expansion should be used somewhere?

 

[Chestermiller]

Thanks for your reply. Could you please hint me on how the first approximation for H can be achieved. I suppose since you mentioned for r small compared to the radii of the spheres, Taylor expansion should be used somewhere?

Yes. Let P be a horizontal plane tangent to the larger sphere b at its base. We wish to determine the elevation $z_b$ of the surface of b above the plane P as a function of the radial distance r measured from the vertical axis of the sphere. If we draw an appropriate right triangle in the diagram, we can use the Pythagorean theorem to show that $$(b-z_b)^2+r^2=b^2$$If we linearize this with respect to $z_b$, we find that: $$z_b=\frac{r^2}{2b}$$Similarly, for the sphere a, we find that the elevation of its surface above the plane P (tangent to b) is
$$z_a=h+\frac{r^2}{2a}$$Therefore, the gap between the two surfaces H(r) is given by
$$H(r)=z_a-z_b=h+\frac{r^2}{2a}-\frac{r^2}{2b}$$

 

[JyJ]

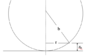
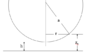
Yes. Let P be a horizontal plane tangent to the larger sphere b at its base. We wish to determine the elevation $z_b$ of the surface of b above the plane P as a function of the radial distance r measured from the vertical axis of the sphere. If we draw an appropriate right triangle in the diagram, we can use the Pythagorean theorem to show that $$(b-z_b)^2+r^2=b^2$$If we linearize this with respect to $z_b$, we find that: $$z_b=\frac{r^2}{2b}$$Similarly, for the sphere a, we find that the elevation of its surface above the plane P (tangent to b) is
$$z_a=h+\frac{r^2}{2a}$$Therefore, the gap between the two surfaces H(r) is given by
$$H(r)=z_a-z_b=h+\frac{r^2}{2a}-\frac{r^2}{2b}$$

I am a bit confused as to why there is a minus sign in H(r) (the answer for the force has a plus).

What I did is the following: if we position the spheres vertically, I thought of looking at the gap between the two spheres in a way that we move the bigger sphere upwards and the smaller one downwards. In that case:
$$ H(r) = z_{a} + z_{b} + h = h + \frac{r^2}{2a} + \frac{r^2}{2b}$$

If we move the bigger sphere upwards - that corresponds to the first part of the calculation you have indicated.
If I understood it correctly, you then lift the smaller sphere closer to the plane and I do not see how the distance to the plane P can be:
$$z_{a} = h +\frac{r^2}{2a}$$ which is bigger than h (which I do not understand how this is possible: if we lift it by more than h and then say that H(r) = z_a - z_b that means the spheres will intersect). In addition, if we lift the smaller sphere upwards, I do not understand how we calculate the distance it was raised by. I would draw a right angle triangle having the origin of the smaller sphere as one of the vertices but then the hypotenuse will be leaving the radius of the sphere, making it difficult to find it.

If I proceed by lifting the bigger sphere and moving the smaller one downwards, as I mentioned before, I get:
$$ H(r) = z_{a} + z_{b} + h = h + \frac{r^2}{2a} + \frac{r^2}{2b}$$
Then, if I attempt to find the volume of fluid in that gap (i.e. right underneath the spheres), the volume that the fluid occupies looks like a frustum cone. Then using its formula for the volume, I find:

$$ V = \frac{\pi H(r)}{3} (a^2 + b^2 +ab) $$

However, I do not see why we need to find this volume and how it goes into calculating the resisting force since for that I would suppose we need change in pressure.

I hope it makes sense what I am trying to say - I am just trying to understand the procedure.

 

[Chestermiller]

I am a bit confused as to why there is a minus sign in H(r) (the answer for the force has a plus).

The answer you gave has a typo in it. The plus sign should obviously be a minus sign. Here are two figures for determining the distance of the surface of each sphere above the bottom plane.

We are not moving the two spheres around anywhere yet. From these two figures, the gap between the two spheres is
$$H(r)=z_a-z_a=h+\frac{r^2}{2a}-\frac{r^2}{2b}$$ The only parameter that is changing with time is h.

However, I do not see why we need to find this volume and how it goes into calculating the resisting force since for that I would suppose we need change in pressure.

You will see in a little while why finding the volume of fluid in the gap between r = 0 and arbitrary radial location r makes solving this problem so much simpler. This volume is given by:$$V=\int_0^r{2\pi rH(r) dr}$$Please do the integration and show what you get. Then determine the derivative of V with respect to time (holding r constant) to get the rate of change of volume V in the gap between r = 0 and arbitrary radial position r.

 

[JyJ]

The answer you gave has a typo in it. The plus sign should obviously be a minus sign. Here are two figures for determining the distance of the surface of each sphere above the bottom plane.

View attachment 236351

View attachment 236364
We are not moving the two spheres around anywhere yet. From these two figures, the gap between the two spheres is
$$H(r)=z_a-z_a=h+\frac{r^2}{2a}-\frac{r^2}{2b}$$ The only parameter that is changing with time is h.
You will see in a little while why finding the volume of fluid in the gap between r = 0 and arbitrary radial location r makes solving this problem so much simpler. This volume is given by:$$V=\int_0^r{2\pi rH(r) dr}$$Please do the integration and show what you get. Then determine the derivative of V with respect to time (holding r constant) to get the rate of change of volume V in the gap between r = 0 and arbitrary radial position r.

Thanks for the corrections. I misunderstood what z_a is at first. I have calculated the volume again:
$$ V = \pi r^2 (h+\frac{r^2}{4}(\frac{1}{a}-\frac{1}{b}))$$
Then, the rate of change of volume becomes:
$$ \frac{dV}{dt} = \pi r^2 \frac{dh}{dt}$$
Could you please advise why we need it?

 

[Chestermiller]

Thanks for the corrections. I misunderstood what z_a is at first. I have calculated the volume again:
$$ V = \pi r^2 (h+\frac{r^2}{4}(\frac{1}{a}-\frac{1}{b}))$$
Then, the rate of change of volume becomes:
$$ \frac{dV}{dt} = \pi r^2 \frac{dh}{dt}$$
Could you please advise why we need it?

Excellent. We need it because the fluid is considered incompressible, so all the fluid volume that is squeezed out of the gap between the spheres in the region between r = 0 and arbitrary r must be flowing out of the region through the surface at r = r, of cross sectional area $2\pi r H$. This enables us to calculate the average radial velocity of the fluid flow in the gap $\bar{v}_r$ at radial location r = r: $$2\pi r H\bar{v}_r=-\frac{dV}{dt}$$So, if you combine these equations, what do you get for $\bar{v}_r$?

 

[JyJ]

Excellent. We need it because the fluid is considered incompressible, so all the fluid volume that is squeezed out of the gap between the spheres in the region between r = 0 and arbitrary r must be flowing out of the region through the surface at r = r, of cross sectional area $2\pi r H$. This enables us to calculate the average radial velocity of the fluid flow in the gap $\bar{v}_r$ at radial location r = r: $$2\pi r H\bar{v}_r=-\frac{dV}{dt}$$So, if you combine these equations, what do you get for $\bar{v}_r$?

Ahh, I see. I get that:

$$v_r = \frac{r\frac{dh}{dt}}{2(\frac{r^2}{2}(\frac{1}{b}-\frac{1}{a} - h)}$$

Should I now use this in the Navier Stokes equation (without inertial terms) to find pressure?

 

[Chestermiller]

Ahh, I see. I get that:

$$v_r = \frac{r\frac{dh}{dt}}{2(\frac{r^2}{2}(\frac{1}{b}-\frac{1}{a} - h)}$$

Should I now use this in the Navier Stokes equation (without inertial terms) to find pressure?

This is correct, aside from the fact that you are missing an inner parenthesis ).

Well, at this point, you know the gap velocity $\bar{v}_r$ and the gap opening H, so you know from lubrication flow that the pressure gradient is given by:
$$\frac{dp}{dr}=-\frac{12\mu \bar{v}_r}{H^2}$$ So, if you combine these equations, what do you get?

 

[Chestermiller]

Incidentally, in deriving the equation I presented in my previous post, unlike what you claimed in post #1, one does need to take into account the $\theta$ components of the forces, and they don't cancel out. What I'm talking about here is a force balance on the section of gap between r and r + dr, and between $\theta$ and $\theta + d\theta$.

 

[JyJ]

Incidentally, in deriving the equation I presented in my previous post, unlike what you claimed in post #1, one does need to take into account the $\theta$ components of the forces, and they don't cancel out. What I'm talking about here is a force balance on the section of gap between r and r + dr, and between $\theta$ and $\theta + d\theta$.

I thought the pressure would not have the $\theta$ component because of the symmetry and so there will be no $\theta$ component of the force as well. If $\theta$ is included I am stooped of what to do. I would assume in that case the flow velocity would have the tangential component, and $2\pi rH v_r = -\frac{dV}{dt}$ would no longer be valid.
As per what we did before, without $\theta$ I got that:
$p = -\frac{6\mu}{H^2} \frac{1}{(\frac{1}{b}-\frac{1}{a})} \frac{dh}{dt} ln|r^2(\frac{1}{b}-\frac{1}{a})-2h|+C$

 

[Chestermiller]

I thought the pressure would not have the $\theta$ component because of the symmetry and so there will be no $\theta$ component of the force as well. If $\theta$ is included I am stooped of what to do.

It goes like this: If we do a force balance on the section of gap channel between r and $r+\Delta r$, and $\theta$ and $\theta+\Delta \theta$, we obtain:
$$[pr\Delta \theta H]_r\mathbf{i_r}-[pr\Delta \theta H]_{r+\Delta r}\mathbf{i_r}+\frac{[pr\Delta \theta]_r+[pr\Delta \theta]_{r+\Delta r}}{2}(H(r+\Delta r)-H(r))\mathbf{i_r}-2\tau_wr\Delta r\Delta \theta \mathbf{i_r}+[pH\Delta r \mathbf{i_{\theta}}]_{\theta}-[pH\Delta r \mathbf{i_{\theta}}]_{\theta+\Delta \theta}=0$$

The terms $[pr\Delta \theta H]_r\mathbf{i_r}-[pr\Delta \theta H]_{r+\Delta r}\mathbf{i_r}$ represent the forces exerted by the fluid in the gap behind and in front of the fluid in the control volume

The term $\frac{[pr\Delta \theta]_r+[pr\Delta \theta]_{r+\Delta r}}{2}(H(r+\Delta r)-H(r))\mathbf{i_r}$ represents the radial component of the pressure force from the diverging channel wall on the fluid in the control volume

The term $-2\tau_wr\Delta r\Delta \theta \mathbf{i_r}$ represents the viscous drag force at the wall on the fluid in the control volume

The terms $[pH\Delta r \mathbf{i_{\theta}}]_{\theta}-[pH\Delta r \mathbf{i_{\theta}}]_{\theta+\Delta \theta}$ represent the pressure forces in the $\theta$ direction on the fluid in the control volume. Because of the curvature of the control volume, these forces have a net component in the radial direction (as we shall soon see).

If we divide the force balance equation by $r\Delta r \Delta \theta$ and take the limit as $\Delta r$ and $\Delta \theta$ approach zero, we obtain:
$$-\frac{1}{r}\frac{d(prH)}{dr}\mathbf{i_r}+p\frac{dH}{dr}\mathbf{i_r}-2\tau_w\mathbf{i_r}-\frac{pH}{r}\frac{d\mathbf{i_{\theta}}}{d\theta}=0$$But, $$\frac{d\mathbf{i_{\theta}}}{d\theta}=-\mathbf{i_{r}}$$Substituting this into the previous equation gives the radial force balance:
$$-\frac{1}{r}\frac{d(prH)}{dr}+p\frac{dH}{dr}-2\tau_w+\frac{pH}{r}=0$$If we differentiate the first term by the product rule, we then finally obtain:
$$-\frac{dp}{dr}=\frac{2\tau_w}{H}=\frac{12\mu v_r}{H^2}$$

I would assume in that case the flow velocity would have the tangential component, and $2\pi rH v_r = -\frac{dV}{dt}$ would no longer be valid.

$v_r$ is the tangential velocity.

As per what we did before, without $\theta$ I got that:
$p = -\frac{6\mu}{H^2} \frac{1}{(\frac{1}{b}-\frac{1}{a})} \frac{dh}{dt} ln|r^2(\frac{1}{b}-\frac{1}{a})-2h|+C$

This is not integrated correctly. H is a function of r, and this has to be taken into account in the integration.