Magnetic field at a point along the solenoid's axis but outside the solenoid

[turo_loler]

TL;DR

For a personal project, I need to calculate the EMF induced by a solenoid, the problem is, that the secondary circuiit where the eddy currents are formed are outside the solenoid's length but on it's axis.

For a personal project, I need to calculate the EMF induced by a solenoid, the problem is, that the secondary circuit where the eddy currents are formed are outside the solenoid's length but still on it's axis.
The problem comes when i need to calculate the vector magnetic field inductance at a point outside the solenoid, i've been searching for quite a while but I have not managed to find an awnser, I just find keep finding that the net magnetic field vector due to ampere's law is near zero, but outsithe the radious of the solenoid, not ousithe the length of the solenoid
A graphical representation of my problem:

 

[Meir Achuz]

In Gaussian units, B is
$$B=\frac{2\pi nI}{c}\left[\frac{L/2-z}{\sqrt{(z-L/2)^2+a^2},
+\frac{(z+L/2)}{\sqrt{(z+L/2)^2+a^2}}\right]$$,
where $n$ is the number of turns per cm, $I$ is the current, $a$ is the radius, and $z$ is the distance along the axis from the center.
Why isn't latex working?

 

[Ibix]

TL;DR Summary: For a personal project, I need to calculate the EMF induced by a solenoid, the problem is, that the secondary circuiit where the eddy currents are formed are outside the solenoid's length but on it's axis.

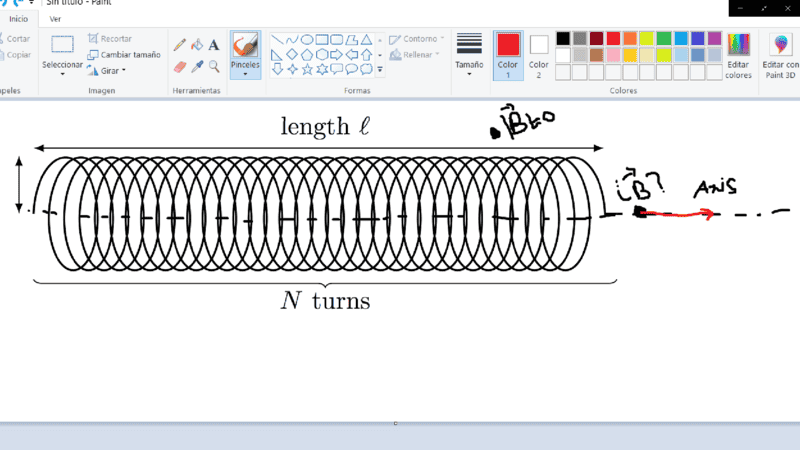
The problem comes when i need to calculate the vector magnetic field inductance at a point outside the solenoid

Google the magnetic field in axis of a current loop a distance $z$ from the loop (the off-axis field is moderately nasty but the on axis field is a simple expression). Then work out how many turns per unit length you have and integrate over the length of the solenoid.

Why isn't latex working?

You have unbalanced {} in the denominator of the first fraction inside the square brackets.

 

[vanhees71]

In Gaussian units, B is
$$B=\frac{2\pi nI}{c}\left[\frac{L/2-z}{\sqrt{(z-L/2)^2+a^2}}
+\frac{(z+L/2)}{\sqrt{(z+L/2)^2+a^2}}\right]$$,
where $n$ is the number of turns per cm, $I$ is the current, $a$ is the radius, and $z$ is the distance along the axis from the center.
Why isn't latex working?

It was a missing bracket in the first frac.

 

[turo_loler]

Google the magnetic field in axis of a current loop a distance $z$ from the loop (the off-axis field is moderately nasty but the on axis field is a simple expression). Then work out how many turns per unit length you have and integrate over the length of the solenoid.

You have unbalanced {} in the denominator of the first fraction inside the square brackets.

Perfect, just what i needed, thnks!

 

[sk_astroman]

May this link help you..
https://www.physicsforums.com/threads/magnetic-field-inside-a-solenoid.981990/