Magnetic field at the center of 3 wires carrying current?

[Helly123]

Homework Statement

each wire carrying 10 Amps
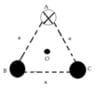
a = 0.3 meter
point o located in the center

Homework Equations

B = permeability constant * I / ( 2 $\pi$ r)
r = distance between O and the wire
r perpendicular to B and I
A = carrying current into the page
B and C = out of the pages

The Attempt at a Solution

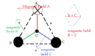
r = 1/2 $\sqrt {a^2 - (1/2a)^2} = (a \sqrt{3} )/4 meter = ((0.3) \sqrt{3})/4$

$({B_{B+C}})^2= {B_{B}}^2 + {B_{C}}^2 + 2{B_{B}}{B_{C}} \cos 120$
$(B_{B+C})$ = Bmagnticfield $\sqrt3$
$(B_{A})$ = Bmagneticfield

Bmagneticfield total = Bmagnticfield $\sqrt3$ + Bmagnticfield
Bmagnticfield = permeability constant * I / ( 2 $\pi$ r)

but I get wrong answer..

can you please help me ?

 

[QuantumQuest]

The field due to the flow of current in wires B and C is opposite in direction to the one of wire A. Now, if you calculate $r$ using Pythagorean theorem and properties of equilateral triangle it's just a matter of some substitution which I leave it to you to do.

 

[Helly123]

The field due to the flow of current in wires B and C is opposite in direction to the one of wire A. Now, if you calculate $r$ using Pythagorean theorem and properties of equilateral triangle it's just a matter of some substitution which I leave it to you to do.

Ok. So, is the r = 0.3$\sqrt3$/4 meter?
So the calculation is $B_B + B_C - B_A$ ?

 

[QuantumQuest]

Ok. So, is the r = 0.3$\sqrt3$/4 meter?

No. How did you find this?

So the calculation is $B_B + B_C - B_A$?

You are asked to find the total (net) magnetic field. At which point do you calculate this?

 

[Helly123]

No. How did you find this?

A' is a mid point of BC
A-O is 1/2AA'
AA' is the height of right triangle AA'C

You are asked to find the total (net) magnetic field. At which point do you calculate this?

At point O.
B of wire B and C is opposite direction of B of wire A

 

[QuantumQuest]

A' is a mid point of BC
A-O is 1/2AA'

In general "center" is a somewhat vague term for a triangle but in the case of an equilateral triangle "center" is the centroid of the triangle i.e. the point that the three medians intersect. At this same point heights and angle bisectors also intersect. The distance of this point to its respective vertex or to the opposite side is not $\frac{1}{2}$. I think that you should know this but in any case take a look at Wikipedia and find out what is the distance from a vertex to the point $O$.

At point O.

OK, so what is the net magnetic field at $O$? Hint: Check what the problem gives in order to find the magnitude and the direction of the induced magnetic field at $O$.

 

[Helly123]

In general "center" is a somewhat vague term for a triangle but in the case of an equilateral triangle "center" is the centroid of the triangle i.e. the point that the three medians intersect. At this same point heights and angle bisectors also intersect. The distance of this point to its respective vertex or to the opposite side is not $\frac{1}{2}$. I think that you should know this but in any case take a look at Wikipedia and find out what is the distance from a vertex to the point $O$.
OK, so what is the net magnetic field at $O$? Hint: Check what the problem gives in order to find the magnitude and the direction of the induced magnetic field at $O$.

Ok. The distance from A to O is 2/3 of AA'. (Not 1/2)
So d = (a$\sqrt 3$)/3

And current A into the page
B and C out of the page. Based on that info the B induced at point O is 2B and direction is to the left.
B = 2.3 10^-5 T

 

[QuantumQuest]

Ok. The distance from A to O is 2/3 of AA'. (Not 1/2)
So d = (a√33\sqrt 3)/3

Correct.

And current A into the page
B and C out of the page. Based on that info the B induced at point O is 2B and direction is to the left.
B = 2.3 10^-5 T

No. Again, I'll point out two things: first, what is the magnetic field induced at point $O$ from each wire? Note that point $O$ is equidistant from the points $A, B, C$. Second, the field generated by the wires passing at $B$ and $C$ is opposite in direction to the one generated by the wire passing at $A$. So, effectively you have to consider these two things which are about the magnitude and direction of the net magnetic field at point $O$ respectively.

 

[Helly123]

O

Correct.
No. Again, I'll point out two things: first, what is the magnetic field induced at point $O$ from each wire? Note that point $O$ is equidistant from the points $A, B, C$. Second, the field generated by the wires passing at $B$ and $C$ is opposite in direction to the one generated by the wire passing at $A$. So, effectively you have to consider these two things which are about the magnitude and direction of the net magnetic field at point $O$ respectively.

Ok. I guess the magnetic field for B and C is to the left the magnitude is B$\cos\theta$ $\theta$ is pi/4
While B for A is to the left with magnitude B = u*I/(2$\pi$r)

r the same for the 3 wires is 0.3$\sqrt3$/3 = 0.1$\sqrt3$

 

[QuantumQuest]

Ok. I guess the magnetic field for B and C is to the left the magnitude is Bcosθcos⁡θ\cos\theta θθ \theta is pi/4
While B for A is to the left with magnitude B = u*I/(2ππ\pir)

I'll try to clarify things further and help but I can't give the solution. You have to find it. So, again

first, what is the magnetic field induced at point $O$ from each wire? Note that point $O$ is equidistant from the points $A,B,C$

What does the "equidistant from the points $A,B,C$" imply for the magnitude of the magnetic field at point $O$? Aren't the three wires induce the same magnitude of magnetic field at point $O$? Then combine with the second thing

Second, the field generated by the wires passing at $B$ and $C$ is opposite in direction to the one generated by the wire passing at $A$.

If you think about it in terms of simple numbers, it can't be explained further without giving the solution. I think that you can find it.

 

[Helly123]

I'll try to clarify things further and help but I can't give the solution. You have to find it. So, again
What does the "equidistant from the points $A,B,C$" imply for the magnitude of the magnetic field at point $O$? Aren't the three wires induce the same magnitude of magnetic field at point $O$?

It is. But the magnetic field at point B and C doesn't get canceled out, does it? Because in the image i posted, B and C result to resultant to the left? Then, When we say the net magnetic force does it take into account the direction? If yes, i thought that magnetic field at points A B C have resultant direction to the left. Maybe i am wrong too.
Equidistant that is $\frac{a\sqrt3}{3}$ right?

 

[Helly123]

The field due to the flow of current in wires B and C is opposite in direction to the one of wire A. Now, if you calculate $r$ using Pythagorean theorem and properties of equilateral triangle it's just a matter of some substitution which I leave it to you to do.

i still don't get it. B and C is opposite in direction of A. B and C canceled A? That is why i posted $B_B + B_C - B_A$

Wire A current into the page, the magnetic field's direction is clockwise
B and C both currents out of the page, magnetic field is counter-clockwise. But B to northwest and C to southwest

 

[QuantumQuest]

It is. But the magnetic field at point B and C doesn't get canceled out, does it? Because in the image i posted, B and C result to resultant to the left? Then, When we say the net magnetic force does it take into account the direction? If yes, i thought that magnetic field at points A B C have resultant direction to the left. Maybe i am wrong too.

i still don't get it. B and C is opposite in direction of A. B and C canceled A? That is why i posted $B_B + B_C - B_A$

Wire A current into the page, the magnetic field's direction is clockwise
B and C both currents out of the page, magnetic field is counter-clockwise. But B to northwest and C to southwest

The direction of the magnetic field is given by the right hand rule. So, using right hand with thumb pointing to the current flow, the rest of fingers curl in the direction of the magnetic field. So far so good. In our case, we have three parallel wires perpendicular to the plane of page - going into the page at $A$ coming out of the page at $B$ and $C$, which form an equilateral triangle and carry an equal magnitude of current namely $10 A$. So, we have three magnetic fields of equal magnitude that affect the centroid $O$ of the equilateral triangle $ABC$, so each in equal distance from the point $O$ which is $\frac{a}{\sqrt{3}}$. What is the magnitude of each magnetic field? You have the formula to calculate it. Then, how can we take into account the fact that

Second, the field generated by the wires passing at $B$ and $C$ is opposite in direction to the one generated by the wire passing at $A$.

Does this say anything more than the sign of each magnetic field, regarding the calculation of the magnitude of the induced magnetic field at point $O$? If so then what is it?

 

[itfitmewelltoo]

Don't two just cancel out leaving the third? thanks

 

[Helly123]

The direction of the magnetic field is given by the right hand rule. So, using right hand with thumb pointing to the current flow, the rest of fingers curl in the direction of the magnetic field. So far so good. In our case, we have three parallel wires perpendicular to the plane of page - going into the page at $A$ coming out of the page at $B$ and $C$, which form an equilateral triangle and carry an equal magnitude of current namely $10 A$. So, we have three magnetic fields of equal magnitude that affect the centroid $O$ of the equilateral triangle $ABC$, so each in equal distance from the point $O$ which is $\frac{a}{\sqrt{3}}$. What is the magnitude of each magnetic field? You have the formula to calculate it. Then, how can we take into account the fact that

take into account the fact that?
The magnetic field is $\frac{(2\sqrt3)}{3 }10^{-5}$ T for each wire.
Does this say anything more than the sign of each magnetic field, regarding the calculation of the magnitude of the induced magnetic field at point $O$? If so then what is it?[/QUOTE]

 

[Charles Link]

This one does, I think, have a simple solution: If you write the current at A as one unit of current out of, and two units of current into the paper, the magnetic field vectors from the one unit of current out of the paper from all 3 vertices will cancel in the center, with the result that you only need to consider the problem as two units of current into the paper at A. $\\$ The alternative is to carefully sum the components of all 3 vectors. $\\$ Editing: But looking closer at it, you already solved it in the OP, but incorrectly applied the law of cosines. If you look at your vector diagram $B_{B+C}=B_{magnetic \, field}$, without the factor of $\sqrt{3}$, so that adding $B_A$ gives you $B_{total}=2 B_{magnetic \, field}$ to the left , which is what the simple method I mentioned in the first sentence gives you. You essentially solved this in the OP. $\\$(You also made an error though in your calculation of $r$ in the OP, as @QuantumQuest pointed out).

 

[Charles Link]

@Helly123 Please see the "Editing:" comment in the previous post.

 

[Helly123]

This one does, I think, have a simple solution: If you write the current at A as one unit of current out of, and two units of current into the paper, the magnetic field vectors from the one unit of current out of the paper from all 3 vertices will cancel in the center, with the result that you only need to consider the problem as two units of current into the paper at A. $\\$ The alternative is to carefully sum the components of all 3 vectors. $\\$ Editing: But looking closer at it, you already solved it in the OP, but incorrectly applied the law of cosines. If you look at your vector diagram $B_{B+C}=B_{magnetic \, field}$, without the factor of $\sqrt{3}$, so that adding $B_A$ gives you $B_{total}=2 B_{magnetic \, field}$ to the left , which is what the simple method I mentioned in the first sentence gives you. You essentially solved this in the OP. $\\$(You also made an error though in your calculation of $r$ in the OP, as @QuantumQuest pointed out).

Yes. The resultant is 2B? I am still lacking at adding the vectors. Why without the factor $\sqrt3$?
if i add vector by break B into x and y, i get B$\sqrt2$?

 

[Charles Link]

Yes. The resultant is 2B? I am still lacking at adding the vectors. Why without the factor $\sqrt3$?
if i add vector by fract B into x and y, i get B$\sqrt2$?

When you add the two vectors of the magnetic fields from B and C, you make an equilateral triangle with the resultant across the horizontal side. (The resultant is the horizontal diagonal across the middle of the diamond). If you want to calculate this using the law of cosines, the 60 degree angle is at the top of the diamond, and $B_{B+C}$ across the middle: $(B_{B+C})^2=B_B^2+B_C^2-2B_BB_C \cos(60)=2B^2-B^2=B^2$. $\\$ But since it is an equilateral triangle, you really don't need the law of cosines to compute it.

 

[Helly123]

When you add the two vectors, you make an equilateral triangle with the resultant across the horizontal side. If you want to calculate this using the law of cosines, the 60 degree angle is at the top of the diamond, and $B_{B+C}$ across the middle: $(B_{B+C})^2=B_B^2+B_C^2-2B_BB_C \cos(60)=2B^2-B^2=B^2$. $\\$ But since it is an equilateral triangle, you really don't need the law of cosines to compute it.

60 at the top of the diamond? Do you mean at A?
So the magnetic field between B and C creates angle = pi/3 ?

 

[Charles Link]

60 at the top of the diamond? Do you mean at A?
So the magnetic field between B and C creates angle = pi/3 ?

I'm looking at the little vector diagram that you drew to the right of the big triangle with all of the currents. What you labeled in red B+C is the resultant of $B_B+B_C$.

 

[Helly123]

I'm looking at the little vector diagram that you drew to the right of the big triangle with all of the currents.

ok i believe its 60. But how to comprehend it as 60?

 

[Charles Link]

ok i believe its 60. But how to comprehend it as 60?

If you go to your big diagram to the left of it, $\vec{B}_B$ is perpendicular to the line that goes from B to the centroid. Similarly for $\vec{B}_C$. $\\$ All of the angles in these triangles are basically, 30, 60, 90, or 120 degrees, etc., w.r.t. the horizontal. It should be fairly straightforward to compute all of the angles on the diamond of the vector diagram that you sketched to the upper right.$\\$ e.g. Notice the line from B to the centroid bisects the 60 degree angle at the lower left, making a 30 degree angle, etc.

 

[QuantumQuest]

take into account the fact that?

Give post #13 a second reading. I wrote the data of the problem and pointed out the things I did for good reason. I think that the problem is that you are not visualizing the whole thing properly and so you are getting to do unnecessary calculations. I don't say this in an offending way so don't get me wrong. The solution is much simpler than the way you think about it. But at this point I think that I can't say anything more about the solution because I'm on the borderline of giving it away which is of no help to anyone.

 

[Helly123]

Give post #13 a second reading. I wrote the data of the problem and pointed out the things I did for good reason. I think that the problem is that you are not visualizing the whole thing properly and so you are getting to do unnecessary calculations. I don't say this in an offending way so don't get me wrong. The solution is much simpler than the way you think about it. But at this point I think that I can't say anything more about the solution because I'm on the borderline of giving it away which is of no help to anyone.

I am still curious about that "simplest solution" ofc

 

[Helly123]

Does this say anything more than the sign of each magnetic field, regarding the calculation of the magnitude of the induced magnetic field at point $O$? If so then what is it?

That's it. I still don't get it. All i know that the 3 wires induced the same magnetic field.
Second, the direction of current of wire B and C is opposite to wire A. But, How about the direction of the magnetic field?

 

[Helly123]

The direction of the magnetic field is given by the right hand rule. So, using right hand with thumb pointing to the current flow, the rest of fingers curl in the direction of the magnetic field. So far so good. In our case, we have three parallel wires perpendicular to the plane of page - going into the page at $A$ coming out of the page at $B$ and $C$, which form an equilateral triangle and carry an equal magnitude of current namely $10 A$. So, we have three magnetic fields of equal magnitude that affect the centroid $O$ of the equilateral triangle $ABC$, so each in equal distance from the point $O$ which is $\frac{a}{\sqrt{3}}$. What is the magnitude of each magnetic field? You have the formula to calculate it. Then, how can we take into account the fact that
Does this say anything more than the sign of each magnetic field, regarding the calculation of the magnitude of the induced magnetic field at point $O$? If so then what is it?

About the right hand rule, as i stated before B and C is counter-clockwise and A is clockwise. Then, the magnetic field will be perpendicular to the distance to O

 

[vanhees71]

I'd first write everything in terms of vectors. For a current in direction of $z$ the magnetic field is
$$\vec{H}=\frac{I}{2 \pi [(x-x_0)^2+(x-y_0)^2]} \begin{pmatrix} -(x-x_0) \\ y-y_0\\0 \end{pmatrix}.$$
Here $(x_0,y_0)$ are the locations of the wires in the $(x,y)$ plane.

Now you simply add the field vectors from the three currents (of course for the current flowing into the plane (i.a., in $-\vec{e}_x$ direction) you have to flip the sign).

 

[Dadface]

By symmetry the field due to A can be said to be canceled by one of the other fields B or C. That means you only have to find the field due to either C on its own or B on its own. Both fields have the same magnitude and direction at the point in question.

It's just a shortcut suitable for this particular symmetrical set up only. I would advise you to proceed with the other methods being outlined here because they can deal with all arrangements.

 

[QuantumQuest]

@Helly123

The way I know to solve the problem is the one that is implied through my posts on the thread and is shared by other people as well. However, after some more careful analysis and discussion with @Charles Link and after the advice and the very succinct post by @vanhees71 it turns out that the simple solution I implied is rather faulty, so I apologize for this. What matters is if you have understood how things work for the correct solution, as presented by @Charles Link and @vanhees71 and if you finally managed to solve it and found the correct answer according to your textbook.