- #1
xinlan
- 61
- 0
Homework Statement
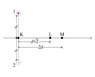
In this problem, you will be asked to calculate the magnetic field due to a set of two wires with antiparallel currents as shown in the diagram . Each of the wires carries a current of magnitude . The current in wire 1 is directed out of the page and that in wire 2 is directed into the page. The distance between the wires is . The x-axis is perpendicular to the line connecting the wires and is equidistant from the wires.
Find the magnitude of the net magnetic field created at point L by both wires.
Express your answer in terms of I,d, and appropriate constants.
Homework Equations
Bwire = uoI/2pid
The Attempt at a Solution
I got the B1L created by wire 1 by point 1 only.
so I thought since they have the same current and distance, they will have the same magnitude, so I just add them. But I got it wrong.
one of the hint says "find the direction of B"
I am confused how to find the direction for wire 1 and 2 at point L.
please someone help me..
Thank you so much..