KedarMhaswade
- 35
- 6
- TL;DR
- A simple pendulum oscillating inside a coil obviously does not generate electricity, or does it?
While reading about electromagnetism from the OpenStax books with my son (and doing some experiments), he asked this question.
Suppose I hang a pendulum and make it oscillate inside a coil connected to a Galvanometer as shown in the schematic diagram:
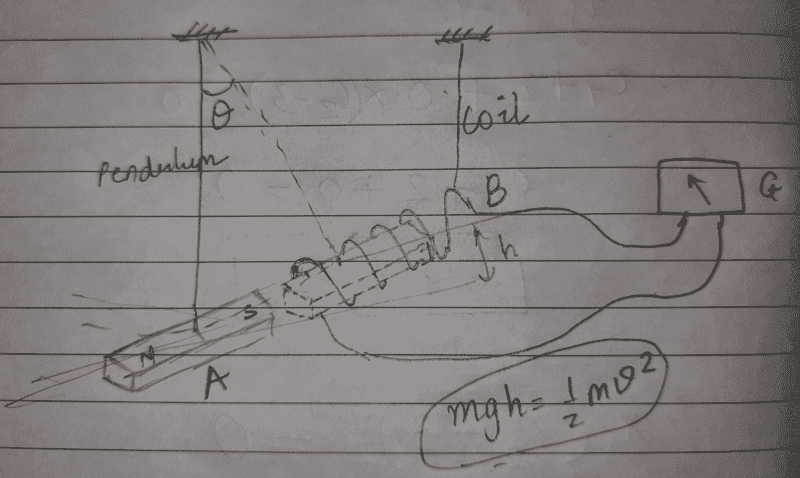
Hopefully the image is clear enough. His argument is that the analysis of the pendulum from Newtonian mechanics suggests that the initial potential energy that I provide to it (##mgh##) is converted into its kinetic energy (##\frac{1}{2} mv^2##). Then the energy dissipates through losses as pendulum eventually comes to a standstill. Thus, the energy I provide in raising the magnet initially is finally lost in friction or to the surrounding air.
But if the magnet is made to oscillate inside a coil, according to Faraday's law, electricity is generated in the coil as the Galvanometer needle shows the deflection. The pendulum does not know that it is made to oscillate inside a coil and it ends up inducing electromotive force in it (as a mere side-effect).
Have I not generated electrical energy violating the law of conservation of energy?
How will you refute this claim?
Does Lenz's law come into the picture and slow down the magnet (since ##F = -\frac{d\phi}{dt}##) which would not have happened had the magnet pendulum not oscillated inside the coil?
Suppose I hang a pendulum and make it oscillate inside a coil connected to a Galvanometer as shown in the schematic diagram:
Hopefully the image is clear enough. His argument is that the analysis of the pendulum from Newtonian mechanics suggests that the initial potential energy that I provide to it (##mgh##) is converted into its kinetic energy (##\frac{1}{2} mv^2##). Then the energy dissipates through losses as pendulum eventually comes to a standstill. Thus, the energy I provide in raising the magnet initially is finally lost in friction or to the surrounding air.
But if the magnet is made to oscillate inside a coil, according to Faraday's law, electricity is generated in the coil as the Galvanometer needle shows the deflection. The pendulum does not know that it is made to oscillate inside a coil and it ends up inducing electromotive force in it (as a mere side-effect).
Have I not generated electrical energy violating the law of conservation of energy?
How will you refute this claim?
Does Lenz's law come into the picture and slow down the magnet (since ##F = -\frac{d\phi}{dt}##) which would not have happened had the magnet pendulum not oscillated inside the coil?