- #1
rocket
- 10
- 0
I'm working on a physics problem, and i got stuck on an integral. the entire question is as follows:
----------------------------
Magnetostatics treats the "source current" (the one that sets up the field) and
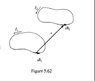
the "recipient current" (the one that experiences the force) so asymmetrically that it is by no means obvious that the magnetic force between two current loops is consistent with Newton"s third law. Show, starting with the Biot-Savart law and the Lorentz force law, that the force on loop 2 due to loop 1 can be written as
[tex] F2 = -\frac{\mu_o}{4\pi}I_1 I_2 \oint_1 \oint_2 \frac{\widehat{r}}{r^2} d\overrightarrow{l_1} \cdot d\overrightarrow{l_2} [/tex]
In this form it is clear that F2 = — F1, since i changes direction when the roles of 1 and 2 are interchanged. (If you seem to be getting an "extra" term, it will help to note that [tex]d\overrightarrow{l_2} \cdot \widehat{r} = dr [/tex].)
--------------------------------------
I'm okay with most of the proof - just a specific part I'm stuck on. i got to the part where i have
[tex] F2 = \frac{\mu_o}{4\pi}I_1 I_2 [\oint_1 \oint_2 \frac{d\overrightarrow{l_1} dr}{r^2} - \oint_1 \oint_2 \frac{\widehat{r}}{r^2} d\overrightarrow{l_1} \cdot d\overrightarrow{l_2}] [/tex]
i want to prove that the first integral is zero, so i need to show that this integral along a closed loop:
[tex]\oint_2 (1/r^2) dr[/tex]
is equal to zero. but I'm not sure how to prove it. i was wondering if someone can show me a rigid proof for this. Note that the integral is along loop 2. Note also that the [tex] \overrightarrow{r} [/tex] is the distance from a point on loop 1 to a point on loop 2 - that is, [tex] \overrightarrow {r} = (x2-x1, y2-y1, z2-z1) [/tex], so in the integral above, where r is a scalar, then [tex]r = [(x2-x1, y2-y1, z2-z1)]^{1/2} [/tex]. I'm not sure how to rewrite dr in terms of x2, since r is a scaler. should it be dr = dxdydz? I think I'm missing something here because I'm not really that familiar with loop integrals.
----------------------------
Magnetostatics treats the "source current" (the one that sets up the field) and
the "recipient current" (the one that experiences the force) so asymmetrically that it is by no means obvious that the magnetic force between two current loops is consistent with Newton"s third law. Show, starting with the Biot-Savart law and the Lorentz force law, that the force on loop 2 due to loop 1 can be written as
[tex] F2 = -\frac{\mu_o}{4\pi}I_1 I_2 \oint_1 \oint_2 \frac{\widehat{r}}{r^2} d\overrightarrow{l_1} \cdot d\overrightarrow{l_2} [/tex]
In this form it is clear that F2 = — F1, since i changes direction when the roles of 1 and 2 are interchanged. (If you seem to be getting an "extra" term, it will help to note that [tex]d\overrightarrow{l_2} \cdot \widehat{r} = dr [/tex].)
--------------------------------------
I'm okay with most of the proof - just a specific part I'm stuck on. i got to the part where i have
[tex] F2 = \frac{\mu_o}{4\pi}I_1 I_2 [\oint_1 \oint_2 \frac{d\overrightarrow{l_1} dr}{r^2} - \oint_1 \oint_2 \frac{\widehat{r}}{r^2} d\overrightarrow{l_1} \cdot d\overrightarrow{l_2}] [/tex]
i want to prove that the first integral is zero, so i need to show that this integral along a closed loop:
[tex]\oint_2 (1/r^2) dr[/tex]
is equal to zero. but I'm not sure how to prove it. i was wondering if someone can show me a rigid proof for this. Note that the integral is along loop 2. Note also that the [tex] \overrightarrow{r} [/tex] is the distance from a point on loop 1 to a point on loop 2 - that is, [tex] \overrightarrow {r} = (x2-x1, y2-y1, z2-z1) [/tex], so in the integral above, where r is a scalar, then [tex]r = [(x2-x1, y2-y1, z2-z1)]^{1/2} [/tex]. I'm not sure how to rewrite dr in terms of x2, since r is a scaler. should it be dr = dxdydz? I think I'm missing something here because I'm not really that familiar with loop integrals.
Attachments
Last edited: