L_landau
- 27
- 0
Homework Statement
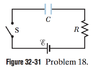
The circuit in Fig. 32-31 consists of switch S, a 12.0 V ideal battery, a 20.0 M resistor, and an air-filled capacitor. The capacitor has parallel circular plates of radius 5.00 cm, separated by 3.00mm. At time t=0, switch S is
closed to begin charging the capacitor. The electric field between the plates is uniform. At t=250 ms, what is the magnitude of the magnetic field within the capacitor, at radial distance 3.00 cm?
Homework Equations
∫ B⋅ds = ε0 dφE/dt
The Attempt at a Solution
I started by looking at dφE/dt. I said dφE/dt = dE/dt * A. Then I said that q = CV and therefore dq/dt = C dV/dt --> dv/dt = I/C. For a parallel plate capacitor we know that ΔV = E*d so taking the derivative dV/dt = dE/dt*d -- > dE/dt = 1/d * dV/dt. I then plug in the previously found dV/dt (=I/C) and since for a parallel capacitor C = ε0 * A/d, dE/dt = 1/d * I*d/ε0*A = I/(ε0*A). I'm quite confused because this gives me units of A*Newtons*m^2/coulombs^2, which is V/m/s. This seems dimensionally incorrect to me. Could anyone point me in the right direction?