Sefrez
- 124
- 0
Homework Statement
There is a frictionless incline with a "block" mass on it. The incline and the mass are able to move. The mass of the block is m and the mass of the incline is M.
I am supposed to find a suitable set of generalized coordinates and write the Lagrangian of the system, then from that, determine equations of motion.
2. The attempt at a solution
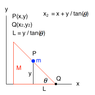
I chose coordinates in a cartesian frame to describe the position of the block mass. (x, y)
From this, I constrained the incline so that it is "in contact" with the block mass at all times (assuming the block to be a point mass):
(x2,y2) = (x1 + y1/tan(θ), 0)
where this is measured from the end of the inclination at some x and y = 0. θ is the angle from the horizontal.
I then constructed the Lagrange function:
L = (1/2)m((d/dt x)^2 + (d/dt y)^2) + (1/2)M(d/dt(x1 + y1/tan(θ)))^2 - mgy
where the last term is the potential of the block measured from the zero potential at y = 0. The inclination should have no potential term as it never moves along the direction of the conservative field, gravity (its height is constant.)
I computed the equations of motion, and they are incorrect. What am I doing wrong? Given (x, y) of the block mass, the position of the incline is fully defined and so it seems I have fully described the system. Any help is appreciated, this problem is driving me nuts!