Mass Spectroscopy: Difference in potential

[hbc.football2]

Homework Statement

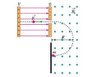
A Mass-spectrometer consists of cylindrical capacitor with inner radius R1=4.5 cm and outer radius R2=5.1cm. Ions enter the mass-spectrometer through a narrow slit which is situated in between the capacitor plates as shown on the picture. Uniform magnetic field B=0.4 T is applied parallel to the capacitor’s axis, direction out of the plane. Find potential difference that should be applied between capacitance’s plates in order for the lithium ion Li+7 (such ions have charge +e, mass 7m, m=1.67*10-27 kg) to go around the middle section of the capacitor, i.e. on the circle of R= 4.8 cm. Energy of incoming ions is 1200 eV. By how much the potential should be changed in order for lithium ions Li+6 to go around the same trajectory?

Homework Equations

Looking through my text I found this info

R= mv/qB

1/2mv^2=eV (V is the accelerating potential)

The Attempt at a Solution

I am pretty sure this is wrong, but I found v using the first equation and then subbed in each velocity to find the accelerating potential for Li+7 and Li+6. I subtracted the accelerating potential of Li+7 from Li+6's to get my final answer. I completely ignored the 1200 eV so I am kind of worried. My final answer was 2946.9V-2525.92V=421V.

Thanks.

 

[ehild]

You can get the speed of the incoming ions from the given energy of 1200 eV. Without the electric field, the ions would move along a circle of radius R= mv/qB inside the spectrometer. The electric field between the capacitor plates exerts an extra radial force on the particles so the resultant force gives the centripetal force appropriate to the radius=(4.5+5.1)/2 cm of the desired trajectory.

ehild

 

[hbc.football2]

Okay, so using the 1200 eV I got that Li+7 has a velocity of 181383.34 m/s (I'm assuming) and for Li+6 is 195916.37. With B coming out of the screen I used the right hand rule to see that my Magnetic force was pointing down. This led me to see that since the Li+6 is lighter it will be deflected more so I need a stronger electric field to bring it up?

Would finding the magnetic force by using F=qvB be of any help? I could see how much more force is acting on the particle bringing it down and then translate that into potential energy? by doing E/q=potential?

 

[hbc.football2]

Sorry, I would use Eq=qvB to find E then divide the difference by q from Li+6 to Li+7 to get the potential

 

[ehild]

You need to use F_m=qvB to get the magnetic force, which points towards the centre of the circle. You also need to find the force of the electric field, F_e=qE, so the resultant of these forces is equal to the centripetal force for a circular trajectory with the given radius and speed. You also need to know how voltage of a cylindrical capacitor is related to the potential difference between its plates.
You need to know the potential difference both for Li+7 and Li+6 ions.

ehild

 

[hbc.football2]

Okay,

so I found my magnetic force to be:

LI+7 3.4*10^-40

Li+6 3.145*10^-37

using the F=mv^/r formula for centripetal force I found that:

Li+7: 8.0123*10^-15

and Li+6: 8.0125*10^-15

is needed for a radius of .048.

I'm lost. Should I subtract the magnetic force form the centripetal to see how much electric force I need?

 

[hbc.football2]

Would there be a negative Vab for the Li+6 because once the plates become charged more the potential goes down?

 

[ehild]

Can you show a picture? I do not know what you mean on "down", towards the centre of away from it, and which plate is A and which is B?
You got correct values for the speeds, and for the centripetal force, but the magnetic force is wrong. It is qvB which is about
1.6*10^(-19)*1.8*10^5*0.4, range of 10^(-14) N.
The sum of the magnetic force and qE is equal to Fcp. E can be both negative and positive, depends on Fm if it is to high or to low for the trajectory. From the direction of E you find out which plate is positive.

ehild

 

[hbc.football2]

For some reason I can't get the picture to show up. I tried multiple ways.

The picture is rather simple, it is a rainbow/half donut shape with a path going through which is designated as R (goes from the origin to the path). R1 is the radius of the bottom of the rainbow from the origin and R2 is the radius from the origin through the entire "rainbow". The particle is moving to the right and B is pointing out of the page.

Is that understandable?

 

[hbc.football2]

I found that the Magnetic force for Li+7 is 1.62*10^-14
and for Li+6 is 1.255*10^-14

leaving me with that for Li+7 the electric force needs to equal 8.1877E-15 in the opposite direction of the magnetic force.

and for Li+6 4.5375E-15 in the opposite direction of the magnetic force.

 

[hbc.football2]

There is no distinction between plate A and plate B.

 

[hbc.football2]

This is similar except the semicircular chamber is closed flip the picture counterclockwise 90 degrees.

 

[ehild]

So downward means toward the centre. OK.

From the force, you get the electric field strength. You need to find the formulae both for the electric field inside and the potential difference across a cylindrical capacitor (or derive them).

ehild

 

[hbc.football2]

I'm a little confused on how to find the potential between the plates because I am not given any explicit information about the plates themselves.

Can I use the integral of E(dot)dl from a to b to find the electric potential?

 

[hbc.football2]

are you finding electric field strength from F=Eq?

Is the q the charge of the ion?

 

[ehild]

are you finding electric field strength from F=Eq?

Is the q the charge of the ion?

Yes.

ehild

 

[hbc.football2]

So now that I have E you mentioned finding a formula that has electric potential for the capacitor plates. I looked at all my fomulas and couldn't find a capacitor related equation that would work because of my limited data. Could I use E/q=v?

 

[ehild]

See the formula for the potential difference ΔV: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capcyl.html

ehild

 

[hbc.football2]

Can I use E to find lambda? E=lambda/2(pi)(epsilon-nought)r?

and then plug it into the equation to find delta V? How else would I find the charge density of the capacitor plates?

 

[ehild]

Can I use E to find lambda? E=lambda/2(pi)(epsilon-nought)r?

and then plug it into the equation to find delta V? How else would I find the charge density of the capacitor plates?

Yes.

ehild

 

[hbc.football2]

would my r be .003 meters because that's the distance from the radius of the traveling particle?

 

[ehild]

You got E at the radius of the circular trajectory, r=0.048 m.

ehild

 

[hbc.football2]

So I think I am seeing the end of the problem

I can plug in the E for Li+7 to find lambda which then will help me find delta V

then plug in the E for Li+6 to find lambda which will then find that particular delta V

which means that I will need to reduce my potential for the Li+6 so my answer will be Li+6-Li+7 to get a negative result (to show that it has to go lower)

 

[hbc.football2]

for my final answer I got that the potential should be lowered by 2.193E-17 V for the Li+6 to travel the same path.

 

[ehild]

I do not think it is correct. What did you get for the electric field needed for the LI+7 ion?

As the concentric cylinders are fairly close, you can consider the electric field constant between them as first approximation, and find the voltage between the concentric plates as ΔV=E D, where D is the distance between the inner and outer cylinders.

ehild

 

[hbc.football2]

I got that the electric field should equal 8.1877E-15 for Li+7

because 1.62E-14-8.1877E-15= centripetal force 8.0123E-15

 

[ehild]

I got that the electric field should equal 8.1877E-15 for Li+7

because 1.62E-14-8.1877E-15= centripetal force 8.0123E-15

It is the electric force, which is F_e=E*e. You need E.

ehild