Mass-spring-damper system "shock absorber"

[vaitus]

Homework Statement

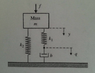
Find equations of motion for mechanical system given by picture, where m = 1kg, k1 = 10, k2 = 25, b = 3 and natural lengths of springs are a1 = 1m, a2 = 2m. The whole system is in a gravitational field g = 9.81m/s^2

Homework Equations

The Attempt at a Solution

I came up with
$$m\ddot{y} = -k_2 y + k_1 (q-y) + mg \\ b\dot{q} = -k_1(q-y)$$
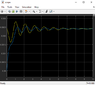
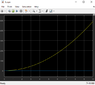
but whenever I try to model it in simulink it doesn't seem right.

 

[BvU]

it doesn't seem right

In what respect ?

Anyway, you can check what you get for k₁=0 and for k₂=0

 

[vaitus]

When I let k1=k2=0 the mass will just keep falling, which is ok (second picture). But when k1, k2 is what it should be then (second pic), I would guess they shouldn't have an equilibrium state at the same place.

EDIT: Oh, It should be this way because it isn't the position but it's displacement and when it doesn't have mass (the q) then it should be this.
Ok, anyway thanks