Maximize Viewing Angle: Find the Perfect Seat for Your Date

[MarkFL]

Suppose you have taken your sweetheart to see the latest blockbuster, and you wish to impress your date by optimizing your viewing angle $\beta$ to the screen. You go to the theater in advance of the date and take some measurements. But being a true mathematician, you decide to generalize and develop a formula that will work for any theater.

When in the front row, your date's eye level is $h$ units below the bottom of the screen. The rows of seats are inclined up at an angle of $0\le\theta<\dfrac{\pi}{2}$, and there is an aisle of width $w$ between the front row and the wall on which the screen is placed. The height of the screen is $S$. Here is a sketch of the arrangement:

View attachment 1185

What horizontal distance from the screen maximizes your viewing angle? Be advised, before being seated, your date will expect that you can prove the distance you suggest is the maximum for $\beta$. (Tongueout)

 

[Mathwebster]

No, your date will insist that you buy her popcorn. (Bigsmile)

 

[anemone]

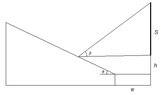
If we translate everything that we're told in a Cartesian diagram and by assigning the bottom of the screen as the origin point, we then get

View attachment 1197
[TABLE="class: grid, width: 500"]
[TR]
[TD]The gradient of the straight line that connects the point $(-w-x, x\tan \theta-h)$ and $(0, 0)$ is $$\tan k^{\circ}=\frac{x\tan \theta-h}{-w-x}=\frac{h-x\tan \theta}{w+x}$$[/TD]
[TD]The gradient of the straight line that connects the point $(-w-x, x\tan \theta-h)$ and $(0, S)$ is $$\tan m^{\circ}=\frac{x\tan \theta-h-S}{-w-x}=\frac{h+S-x\tan \theta}{w+x}$$[/TD]
[/TR]
[TR]
[TD]Hence, $$k^{\circ}=arc \tan \left(\frac{h-x\tan \theta}{w+x}\right)$$[/TD]
[TD]Hence, $$m^{\circ}=arc \tan \left(\frac{h+S-x\tan \theta}{w+x}\right)$$[/TD]
[/TR]
[/TABLE]

Therefore, the viewing angle, $\beta$ is

$$\beta^{\circ}=m^{\circ}-k^{\circ}=arc \tan \left(\frac{h+S-x\tan \theta}{w+x}\right)-arc \tan \left(\frac{h-x\tan \theta}{w+x}\right)$$

One of the credible ways to maximize the viewing angle $\beta$ is through the differentiation method.

$$\frac{d\beta}{dx}=\frac{d \left( arc \tan \left(\frac{h+S-x\tan \theta}{w+x}\right)\right)}{dx}-\frac{d \left(arc \tan \left(\frac{h-x\tan \theta}{w+x}\right)\right)}{dx}$$

$$\;\;\;\;\;\;=\left(\small\frac{1}{1+\left(\frac{h+S-x\tan \theta}{w+x}\right)^2}\right)\left(\tiny\frac{(-\tan x)(w+x)-h-S+x\tan \theta}{(w+x)^2}\right)-\left(\small\frac{1}{1+\left(\frac{h+S-x\tan \theta}{w+x}\right)^2}\right)\left(\small\frac{(-\tan x)(w+x)-h-S+x\tan \theta}{(w+x)^2}\right)$$

$$\;\;\;\;\;\;=\left(\frac{-w\tan \theta-h-S}{(w+x)^2+(h+S-x\tan \theta)^2}\right)-\left(\frac{-w\tan \theta-h}{(w+x)^2+(h-x\tan \theta)^2}\right)$$

$$\;\;\;\;\;\;=\left(\frac{P-S}{Q+(R+S)^2}\right)-\left(\frac{P}{Q^2+R^2}\right)$$

$$\;\;\;\;\;\;=\left(\frac{PQ^2+PR^2-SQ^2-SR^2-PQ^2-PR^2-2PRS-PS^2}{(Q+(R+S)^2)(Q^2+R^2)}\right)$$

$$\;\;\;\;\;\;=\left(\frac{-S(Q^2+R^2+2PR+PS)}{(Q+(R+S)^2)(Q^2+R^2)}\right)$$

where

$P=-w\tan \theta-h$, $Q=w+x$, and $R=h-x\tan \theta$.

Keep in mind that our aim is to find for the corresponding $x$ value when maximum $\beta$ occurs.

i.e. we need to equate $\frac{d\beta}{dx}=0$ and this can be achieved only when $Q^2+R^2+2PR+PS=0$, in other words, what we're dealing now is

$$(w+x)^2+(h-x\tan \theta)^2+2(-w\tan \theta-h)(h-x\tan \theta)+S(-w\tan \theta-h)=0$$

Solving this for $x$, we have

$$w^2+2wx+x^2+h^2-2hxtan \theta+x^2\tan^2 \theta-2(w\tan \theta+h)(h-x\tan \theta)-S(w\tan \theta+h)=0$$

$$\small x^2\sec^2 \theta+2x(w-h\tan \theta+w\tan^2 \theta+h\tan \theta)+w^2+h^2-2(w\tan \theta+h)+2x\tan \theta(w\tan\theta+h)-Sw\tan \theta-Sh=0$$

$$x^2\sec^2 \theta+2x(w\sec^2 \theta)+w^2-h^2-Sh-w\tan \theta(S+2h)=0$$

Quadratic formula tells us

$$x=\frac{-2w\sec^2 \theta \pm \sqrt{4w^2\sec^4 \theta-4\sec^2 \theta(w^2-h^2-Sh-w\tan \theta(S+2h))}}{2\sec^2 \theta}$$

$$x=-w\pm\frac{\sqrt{w^2\sec^2 \theta- (w^2-h^2-Sh-w\tan \theta(S+2h))}}{\sec \theta}$$

$$x=-w\pm\frac{\sqrt{w^2\tan^2 \theta+h^2+Sh-Sw\tan \theta+2hw\tan \theta}}{\sec \theta}$$

$$x=-w\pm\frac{\sqrt{(w\tan \theta+h)^2+S(h+w\tan \theta)}}{\sec \theta}$$

$$x=-w\pm\frac{\sqrt{(w\tan \theta+h)(h+w\tan \theta+S)}}{\sec \theta}$$

That is,

[TABLE="width: 500"]
[TR]
[TD]$$x=-w+\frac{\sqrt{(w\tan \theta+h)(h+w\tan \theta+S)}}{\sec \theta}$$[/TD]
[TD]or[/TD]
[TD]$$x=-w-\frac{\sqrt{(w\tan \theta+h)(h+w\tan \theta+S)}}{\sec \theta}$$[/TD]
[/TR]
[/TABLE]

We can conclude that $$x=-w+\frac{\sqrt{(w\tan \theta+h)(h+w\tan \theta+S)}}{\sec \theta}$$ is the right answer (without needing to prove if this point generates the maximum value for $\beta$) because we can tell from the diagram that $-(x+w)<0$ and hence, you and your sweetheart should sit $$\frac{\sqrt{(w\tan \theta+h)(h+w\tan \theta+S)}}{\sec \theta}$$away from the screen in order to get the maximize viewing angle!:)

 

[MarkFL]

Thank you anemone for your response. (Clapping)

I took a classic problem in elementary calculus and "tweaked" it a bit to both make it more realistic, and as added realism often does, more difficult. Here is my solution:

I oriented the origin of the coordinate axes at the front row viewing position, with the positive horizontal direction taken to the left. I found the slopes of the rays from the origin to the top and bottom of the screen, and used these to state:

$$\beta(x)=\tan^{-1}\left(\frac{S+h-x\tan(\theta)}{x+w} \right)-\tan^{-1}\left(\frac{h-x\tan(\theta)}{x+w} \right)$$

Next, I differentiated with respect to $x$ and equated to zero to find the critical point(s):

$$\beta'(x)=\frac{h+w\tan(\theta)}{(x+w)^2+(h-x\tan(\theta))^2}-\frac{S+h+w\tan(\theta)}{(x+w)^2+(S+h-x\tan(\theta))^2}=0$$

As we can see, this implies:

$$\left(h+w\tan(\theta) \right)\left((x+w)^2+(S+h-x\tan(\theta))^2 \right)=\left(S+h+w\tan(\theta) \right)\left((x+w)^2+(h-x\tan(\theta))^2 \right)$$

$$\left(h+w\tan(\theta) \right)(S+h+w\tan(\theta)-(x+w)\tan(\theta))^2=S(x+w)^2+ \left(S+h+w\tan(\theta) \right)(h+w\tan(\theta)-(x+w)\tan(\theta))^2$$

$$(h+w\tan(\theta))(S+h+w\tan(\theta))^2= S(x+w)^2+S\tan^2(\theta)(x+w)^2+(h+w\tan(\theta))^2(S+h+w\tan(\theta))$$

$$(x+w)^2=\cos^2(\theta)(h+w\tan(\theta))(S+h+w\tan(\theta))$$

Taking the positive root, we find:

$$x+w=\cos(\theta)\sqrt{(h+w\tan(\theta))(S+h+w\tan(\theta))}$$

Now, since we cannot sit in front of the front row, this will only be a usable maximum if $x$ is non-negative, hence:

$$\cos^2(\theta)(h+w\tan(\theta))(S+h+w\tan(\theta))\ge w^2$$

$$w^2-\tan(\theta)(2h+S)w-h(h+S)\le0$$

Therefore, we find we require:

$$0\le w\le\frac{(2h+S)\tan( \theta)+\sqrt{((2h+S)\tan(\theta))^2+4h(h+S)}}{2}$$

Because:

$$\lim_{x\to\infty}\beta(x)=0$$

We know then if the above condition is met, then our critical value is a maximum.

Thus, in conclusion, when we find:

$$0\le w\le\frac{(2h+S)\tan( \theta)+\sqrt{((2h+S)\tan(\theta))^2+4h(h+S)}}{2}$$

Then the optimal horizontal distance from the screen is:

$$x+w=\cos(\theta)\sqrt{(h+w\tan(\theta))(S+h+w\tan(\theta))}$$

Otherwise, we want:

$$x+w=w$$