megaforcetkd
- 22
- 0
Homework Statement
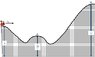
A frictionless roller coaster is given an initial velocity of vo at a height of h = 85 m, as in figure shown. The radius of curvature of the track at point A is 127 m.
(a) Find the maximum value of vo so that the roller coaster stays on the track at point A solely because of gravity.
(b) Using the value of vo calculated in part (a), determine the value of h' that is necessary if the roller coaster just makes it to point B.
(c) What condition must the radius of curvature be in relation to the height h for this problem to work? Show all work leading to your conclusion.
Homework Equations
Fn = Fg
MEi = MEf
1/2mv1^2 + mgh1 = 1/2mv2^2 + mgh2
The Attempt at a Solution
I don't know how to approach this at all... Never done anything like this.