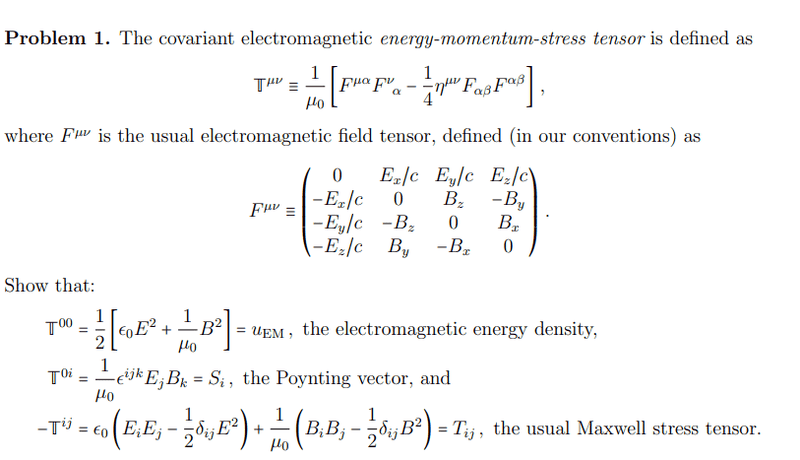Homework Help Overview
The discussion revolves around the components of the energy-stress-momentum tensor in the context of electromagnetism, specifically related to Maxwell's equations and the tensor formulation of electromagnetic fields.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants explore the correct formulation of the tensor components, question the sign conventions used, and discuss the necessity of various tensor components. There are attempts to clarify misunderstandings about the notation and the physical meaning of the components.
Discussion Status
The discussion is active, with participants providing guidance on the correct approach to calculating the tensor components and addressing typographical errors in the problem statement. Multiple interpretations of the problem are being explored, particularly regarding the necessity of certain components and the implications of summing them.
Contextual Notes
There are indications of confusion regarding the indices used in the tensor notation and the assumptions about the physical context, such as the absence of charge density or current density in certain equations.