Bavid
- 31
- 0
Measure of the "Sharpness of a curve"
I have a set of curves that belong to the family of curves y=\frac{c}{x^m}, where m and c are parameters.
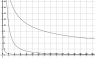
The attached picture (save.png) shows three such curves for different values of m and c.
Now these curves have different 'sharpenss' of curvature (to see what I mean by sharpness, observe how 'sharp' a corner the lowermost curve forms compared to the uppermost).
I am trying to find a function F of m and c that can quantify this sharpness, i.e., larger value of F(m,c) indicates that the corresponding curve has a sharper corner or the vice versa.
Any ideas how to go about constructing the function F?
I have a set of curves that belong to the family of curves y=\frac{c}{x^m}, where m and c are parameters.
The attached picture (save.png) shows three such curves for different values of m and c.
Now these curves have different 'sharpenss' of curvature (to see what I mean by sharpness, observe how 'sharp' a corner the lowermost curve forms compared to the uppermost).
I am trying to find a function F of m and c that can quantify this sharpness, i.e., larger value of F(m,c) indicates that the corresponding curve has a sharper corner or the vice versa.
Any ideas how to go about constructing the function F?