- #1
gfd43tg
Gold Member
- 950
- 50
Hello,
I will be doing an experiment to separate N2 from O2 in air using membrane separations. I need to write my own experimental procedure to find the objectives of the experiment.
Here is our experimental set up
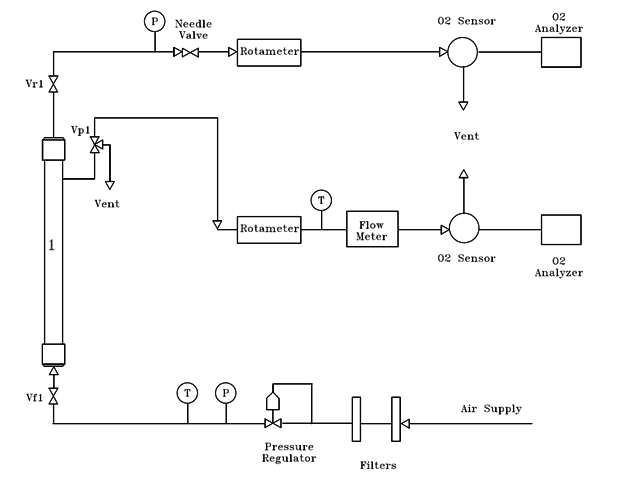
I'm trying to figure out how to do objective i. I need to figure out the selectivity of the membrane for oxygen over nitrogen. It says I should calculate the transmissibility of the two species. the transmissibility, ##k_{pi}## is defined
$$ k_{pi} = \frac {\mathcal{P}_{i}}{L_{m}} $$
Where ##\mathcal{P}_{i}## is the permeability of species ##i##, and ##L_{m}## is the length of the membrane. You can calculate the molar flux, ##J_{i}##
$$ J_{i} = k_{pi}(P_{ir}-P_{ip}) $$
Where ##P_{ir}## is the retentate pressure (feed pressure), and ##P_{ip}## is the permeate pressure. I get I can find the feed pressure from the first gauge, but from the diagram there is no pressure gauge for the permeate. I figured I could calculate the molar flux because the permeate flow rate is equal to the area of the membrane times the average molar flux
$$ V_{p} = A_{T} \langle J_{i} \rangle $$
So I could use the rotameter to find ##V_{p}##, then knowing ##A_{T}## I can calculate the ##\langle J_{i} \rangle##. Once I have ##\langle J_{i} \rangle##, I would do
$$ \langle J_{i} \rangle = k_{pi}(P_{feed}-P_{permeate}) $$
But I run again into the problem of not knowing ##P_{permeate}##. If I can get that, then I know the selectivity is trivial
$$ \alpha_{ij} = \frac {k_{pi}}{k_{pj}} $$
Any ideas how I might be able to do this? One thought is using the temperature of the permeate to find the permeate pressure with the ideal gas law.
I will be doing an experiment to separate N2 from O2 in air using membrane separations. I need to write my own experimental procedure to find the objectives of the experiment.
OBJECTIVES:
i. Determine the membrane selectivity to O2 from measurements of the membrane transmissibility to N2 and O2.
ii. Characterize the membrane to determine how air-separation performance depends on feed pressure, retentate flow rate, and module configuration (i.e., co-current or counter-current).
iii. Develop a mathematical model to predict the dependence of permeate flow rate and purity on the retentate production rate, pressure, and composition, as well as the membrane transmissibilities. Discuss model limitations.
iv. Based on the experimental and model results, recommend optimal operating conditions (pressure, flow rate, module configuration) to produce a >95 mol% N2 product stream. Describe tradeoffs in operating conditions.
Here is our experimental set up
I'm trying to figure out how to do objective i. I need to figure out the selectivity of the membrane for oxygen over nitrogen. It says I should calculate the transmissibility of the two species. the transmissibility, ##k_{pi}## is defined
$$ k_{pi} = \frac {\mathcal{P}_{i}}{L_{m}} $$
Where ##\mathcal{P}_{i}## is the permeability of species ##i##, and ##L_{m}## is the length of the membrane. You can calculate the molar flux, ##J_{i}##
$$ J_{i} = k_{pi}(P_{ir}-P_{ip}) $$
Where ##P_{ir}## is the retentate pressure (feed pressure), and ##P_{ip}## is the permeate pressure. I get I can find the feed pressure from the first gauge, but from the diagram there is no pressure gauge for the permeate. I figured I could calculate the molar flux because the permeate flow rate is equal to the area of the membrane times the average molar flux
$$ V_{p} = A_{T} \langle J_{i} \rangle $$
So I could use the rotameter to find ##V_{p}##, then knowing ##A_{T}## I can calculate the ##\langle J_{i} \rangle##. Once I have ##\langle J_{i} \rangle##, I would do
$$ \langle J_{i} \rangle = k_{pi}(P_{feed}-P_{permeate}) $$
But I run again into the problem of not knowing ##P_{permeate}##. If I can get that, then I know the selectivity is trivial
$$ \alpha_{ij} = \frac {k_{pi}}{k_{pj}} $$
Any ideas how I might be able to do this? One thought is using the temperature of the permeate to find the permeate pressure with the ideal gas law.
Last edited: