- 22,170
- 3,327
Here is a thread of challenges made especially for high school students and first year university students. All the following problems can be solved with algebra, trigonometry, analytic geometry, precalculus and single-variable calculus. That does not mean that the question are all easy.
For non-high schoolers, there is my summer challenges: https://www.physicsforums.com/threads/micromass-big-summer-challenge.879072/
RULES:
1. Suppose that in each individual of a large population there is a pair of genes, each of which can either ##x## or ##X##, that controls eye color: those with ##xx## have blue eyes, while heterzygotes (those with ##Xx## or ##xX##) and those with ##XX## have brown eyes. The proportion of blue eyed individuals is ##p^2## and of heterzygotes is ##2p(1-p)## where ##0<p<1##. Each parent transmits one of its own genes to the child; if the parent is a heterozygote, the probability that it transmiths the gene of type ##X## is ##1/2##.
a) SOLVED BY ProfuselyQuarky Assuming random mating, find the expected proportion of heterzygotes in brown-eyed children of brown-eyed parents. Otherwise stated: consider the population of all brown-eyed people whose two parents are brown-eyed. Find the proportion of heterzygotes in that population.
b) SOLVED BY ProfuselyQuarky Suppose Judy, a brown-eyed child of brown-eyed parents marries a heterozygote, and they have ##n## children, all brown eyed. Find the probability that Judy is a heterzygote and the probability that her first grandchild has blue eyes.
2. a) SOLVED BY MAGNIBORO Prove that
1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{1000000} < 20
b) SOLVED BY MAGNIBORO Find an explicit ##n## such that
1+ \frac{1}{2}+ \frac{1}{3} + ... + \frac{1}{n} > 20
3. Let ##p\neq 0## be a real number. Let ##x_1,...,x_n## be positive real numbers, we define the ##p##-mean as
M_p(x_1,...,x_n) = \sqrt[p]{\frac{1}{n}\sum_{i=1}^n x_i^p}
Note that ##M_1(x_1,...,x_n)## is the usual mean. Prove:
a) SOLVED BY Math_QED ##\lim_{p\rightarrow -\infty} M_p(x_1,...,x_n) = \min\{x_1,...,x_n\}##. We define this as ##M_{-\infty}(x_1,...,x_n)##.
b) SOLVED BY Math_QED ##\lim_{p\rightarrow 0} M_p(x_1,...,x_n) = \sqrt[n]{x_1\cdot ... \cdot x_n}##, the geometric mean. We define this as ##M_0(x_1,...,x_n)##.
c) SOLVED BY Math_QED ##\lim_{p\rightarrow +\infty} M_p(x_1,...,x_n) = \max\{x_1,...,x_n\}##. We define this as ##M_{+\infty}(x_1,...,x_n)##.
d) Prove that for all ##p,q\in \mathbb{R}\cup \{- \infty,+\infty\}## has that ##p\leq q## implies ##M_p(x_1,...,x_n)\leq M_q(x_1,...,x_n)##.
4. Take rational numbers ##\frac{a}{c}<\frac{b}{d}## with ##a,b,c,d\in \mathbb{N}##.
a) SOLVED BY Mastermind01 Prove
\frac{a}{c} < \frac{a+b}{c+d} < \frac{b}{d}
b) Prove that if ##bc - ad = 1##, then ##\frac{a+b}{c+d}## is the simplest fraction in ##\left(\frac{a}{c},\frac{b}{d}\right)## in the sense of having the smallest denominator.
5. SOLVED BY Mastermind01 A light ray falling on a straight line is reflected in the following picture:
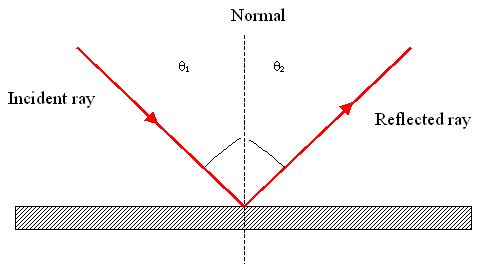
To find the reflected line, we use that ##\theta_1 = \theta_2##.
If a light ray falls on a curve, then it is reflected on the tangent line of the curve:
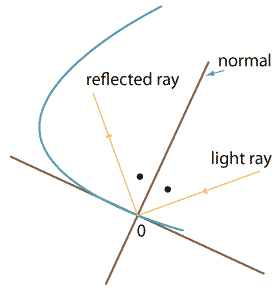
Given the parabola ##y = ax^2 + bx + c##. A light ray comes from ##(h,+\infty)## and follows the vertical line ##x = h##. All such light rays are reflected on the parabola and give rise to reflected light rays. Show that the paths of all the reflected light rays are all concurrent (i.e. they all have a point in common). Find the common point.
6. Find
\sqrt{1 + 2\sqrt{1 + 3\sqrt{1 + 4\sqrt{1 + ...}}}}
7. Let ##C## be the unit circle as defined by ##x^2 + y^2 = 1##. Let ##L_\alpha## be the line through ##(-1,0)## with slope ##\alpha##. A point ##(x,y)\in C## is called rational if both ##x## and ##y## are rational.
a) SOLVED BY Mastermind01 Show that ##L_\alpha## intersects ##C## in a rational point (except for ##(-1,0)##) if and only if ##\alpha## is rational.
b) SOLVED BY MAGNIBORO Find all rational points on the circle. In particular, show there are infinitely such points.
c) SOLVED BY MAGNIBORO Find all positive integers ##a##, ##b## and ##c## such that they can be combined to form a right-angled triangle.
8. SOLVED BY ProfuselyQuarky In a certain school there are ##15## girls. It is desired to make a seven-day schedule such that each day the girls can walk in the garden in five groups of three in such a way that each girl will be in the same group with each other girl just once in the week. How should the groups be formed each day?
9. SOLVED BY MAGNIBORO A donkey is attached by a rope to a point on the perimeter of a circular field. How long should the rope be in terms of the radius of the field so that the donkey can reach exactly half the field and eat half the grass.
10. The same donkey is now tied with a ##50m## long rope. The rope is tied to the corner of a ##20m## by ##10m## barn. What is the total area that the donkey is capable of grazing?
For non-high schoolers, there is my summer challenges: https://www.physicsforums.com/threads/micromass-big-summer-challenge.879072/
RULES:
- In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
- It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
- If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
- You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
1. Suppose that in each individual of a large population there is a pair of genes, each of which can either ##x## or ##X##, that controls eye color: those with ##xx## have blue eyes, while heterzygotes (those with ##Xx## or ##xX##) and those with ##XX## have brown eyes. The proportion of blue eyed individuals is ##p^2## and of heterzygotes is ##2p(1-p)## where ##0<p<1##. Each parent transmits one of its own genes to the child; if the parent is a heterozygote, the probability that it transmiths the gene of type ##X## is ##1/2##.
a) SOLVED BY ProfuselyQuarky Assuming random mating, find the expected proportion of heterzygotes in brown-eyed children of brown-eyed parents. Otherwise stated: consider the population of all brown-eyed people whose two parents are brown-eyed. Find the proportion of heterzygotes in that population.
b) SOLVED BY ProfuselyQuarky Suppose Judy, a brown-eyed child of brown-eyed parents marries a heterozygote, and they have ##n## children, all brown eyed. Find the probability that Judy is a heterzygote and the probability that her first grandchild has blue eyes.
2. a) SOLVED BY MAGNIBORO Prove that
1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{1000000} < 20
b) SOLVED BY MAGNIBORO Find an explicit ##n## such that
1+ \frac{1}{2}+ \frac{1}{3} + ... + \frac{1}{n} > 20
3. Let ##p\neq 0## be a real number. Let ##x_1,...,x_n## be positive real numbers, we define the ##p##-mean as
M_p(x_1,...,x_n) = \sqrt[p]{\frac{1}{n}\sum_{i=1}^n x_i^p}
Note that ##M_1(x_1,...,x_n)## is the usual mean. Prove:
a) SOLVED BY Math_QED ##\lim_{p\rightarrow -\infty} M_p(x_1,...,x_n) = \min\{x_1,...,x_n\}##. We define this as ##M_{-\infty}(x_1,...,x_n)##.
b) SOLVED BY Math_QED ##\lim_{p\rightarrow 0} M_p(x_1,...,x_n) = \sqrt[n]{x_1\cdot ... \cdot x_n}##, the geometric mean. We define this as ##M_0(x_1,...,x_n)##.
c) SOLVED BY Math_QED ##\lim_{p\rightarrow +\infty} M_p(x_1,...,x_n) = \max\{x_1,...,x_n\}##. We define this as ##M_{+\infty}(x_1,...,x_n)##.
d) Prove that for all ##p,q\in \mathbb{R}\cup \{- \infty,+\infty\}## has that ##p\leq q## implies ##M_p(x_1,...,x_n)\leq M_q(x_1,...,x_n)##.
4. Take rational numbers ##\frac{a}{c}<\frac{b}{d}## with ##a,b,c,d\in \mathbb{N}##.
a) SOLVED BY Mastermind01 Prove
\frac{a}{c} < \frac{a+b}{c+d} < \frac{b}{d}
b) Prove that if ##bc - ad = 1##, then ##\frac{a+b}{c+d}## is the simplest fraction in ##\left(\frac{a}{c},\frac{b}{d}\right)## in the sense of having the smallest denominator.
5. SOLVED BY Mastermind01 A light ray falling on a straight line is reflected in the following picture:
To find the reflected line, we use that ##\theta_1 = \theta_2##.
If a light ray falls on a curve, then it is reflected on the tangent line of the curve:
Given the parabola ##y = ax^2 + bx + c##. A light ray comes from ##(h,+\infty)## and follows the vertical line ##x = h##. All such light rays are reflected on the parabola and give rise to reflected light rays. Show that the paths of all the reflected light rays are all concurrent (i.e. they all have a point in common). Find the common point.
6. Find
\sqrt{1 + 2\sqrt{1 + 3\sqrt{1 + 4\sqrt{1 + ...}}}}
7. Let ##C## be the unit circle as defined by ##x^2 + y^2 = 1##. Let ##L_\alpha## be the line through ##(-1,0)## with slope ##\alpha##. A point ##(x,y)\in C## is called rational if both ##x## and ##y## are rational.
a) SOLVED BY Mastermind01 Show that ##L_\alpha## intersects ##C## in a rational point (except for ##(-1,0)##) if and only if ##\alpha## is rational.
b) SOLVED BY MAGNIBORO Find all rational points on the circle. In particular, show there are infinitely such points.
c) SOLVED BY MAGNIBORO Find all positive integers ##a##, ##b## and ##c## such that they can be combined to form a right-angled triangle.
8. SOLVED BY ProfuselyQuarky In a certain school there are ##15## girls. It is desired to make a seven-day schedule such that each day the girls can walk in the garden in five groups of three in such a way that each girl will be in the same group with each other girl just once in the week. How should the groups be formed each day?
9. SOLVED BY MAGNIBORO A donkey is attached by a rope to a point on the perimeter of a circular field. How long should the rope be in terms of the radius of the field so that the donkey can reach exactly half the field and eat half the grass.
10. The same donkey is now tied with a ##50m## long rope. The rope is tied to the corner of a ##20m## by ##10m## barn. What is the total area that the donkey is capable of grazing?
Last edited: