- #1
foo9008
- 678
- 4
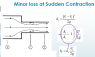
Homework Statement
which formula is correct ? the formula in the first ? or in the second ? one is using the mean velocity , while the another one is using velocity difference between vena contarcta and velocity at exit ...