- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
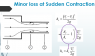
In summary, the minor loss due to sudden expansion is given by the formula [(vc - v2)^2]/2g because the greatest amount of head loss occurs in the zone between station c and station 2, where the velocity vc is greater than v2. This is explained in the Borda-Carnot equation, which states that there is minimal loss between station 1 and station c. The calculation cannot involve vc and v1 as the loss between these two velocities is negligible compared to the loss between vc and v2.
Physics news on Phys.org
- #2
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,811
- 1,671
The graphic talks about head loss due to a sudden contraction.foo9008 said:Homework Statement
why the minor loss due to sudden expansion is given by formula of [( v_c - v_2) ^2 ]/ 2g ?
Homework Equations
The Attempt at a Solution
can it be [( v_2 - v_1) ^2 ]/ 2g ?
The velocity vc is important because it represents the greatest velocity to which the fluid is accelerated as it passes thru the sudden contraction, and consequently, in the zone between station c and station 2 is where the greater amount of head loss occurs. Very little loss occurs in the zone between station 1 and station c.
For more information:
https://en.wikipedia.org/wiki/Borda–Carnot_equation
- #3
foo9008
- 678
- 4
from the link , i can undertstand the gretest amount of energy lost at region c , can the formula be [( v_c - v_1) ^2 ]/ 2g ? how do u know that teh energy loss between c and 2 is greater than the energy loss at (1 and c) ?SteamKing said:The graphic talks about head loss due to a sudden contraction.
The velocity vc is important because it represents the greatest velocity to which the fluid is accelerated as it passes thru the sudden contraction, and consequently, in the zone between station c and station 2 is where the greater amount of head loss occurs. Very little loss occurs in the zone between station 1 and station c.
For more information:
https://en.wikipedia.org/wiki/Borda–Carnot_equation
Last edited:
- #4
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,811
- 1,671
From the velocities. V1 < Vc and Vc > V2, based on the continuity equation. Plus, that's what the wiki article says.foo9008 said:from the link , i can undertstand the gretest amount of energy lost at region c , can the formula be [( v_c - v_1) ^2 ]/ 2g ? how do u know that teh energy loss between c and 2 is greater than the energy loss at (1 and c) ?
- #5
foo9008
- 678
- 4
Can you explain further??SteamKing said:From the velocities. V1 < Vc and Vc > V2, based on the continuity equation. Plus, that's what the wiki article says.
- #6
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,811
- 1,671
What's not clear about "That's what the wiki article says"?foo9008 said:Can you explain further??
- #7
foo9008
- 678
- 4
SteamKing said:What's not clear about "That's what the wiki article says"
It didn't explain why the calculation can't involve vc and v1??
- #8
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,811
- 1,671
Sure it did. You just don't want to accept it, for some reason.
To recap:
"There is not much head loss between cross section 1, before the contraction, and cross section 3, the vena contracta at which the main flow is contracted most. But there are substantial losses in the flow expansion from cross section 3 to 2."
In other words, the loss between v1 and vc is negligible compared to the loss between vc and v2. Since head loss is proportional to velocity squared, the loss caused by the difference in vc and v2 must be based on those two velocities, not on v1 and vc.
To recap:
"There is not much head loss between cross section 1, before the contraction, and cross section 3, the vena contracta at which the main flow is contracted most. But there are substantial losses in the flow expansion from cross section 3 to 2."
In other words, the loss between v1 and vc is negligible compared to the loss between vc and v2. Since head loss is proportional to velocity squared, the loss caused by the difference in vc and v2 must be based on those two velocities, not on v1 and vc.
- #9
foo9008
- 678
- 4
noted
SteamKing said:Sure it did. You just don't want to accept it, for some reason.
To recap:
"There is not much head loss between cross section 1, before the contraction, and cross section 3, the vena contracta at which the main flow is contracted most. But there are substantial losses in the flow expansion from cross section 3 to 2."
In other words, the loss between v1 and vc is negligible compared to the loss between vc and v2. Since head loss is proportional to velocity squared, the loss caused by the difference in vc and v2 must be based on those two velocities, not on v1 and vc.
1. What is meant by "minor loss" in sudden expansion?
Minor loss refers to the decrease in pressure that occurs when a fluid passes through a sudden expansion in a pipe or channel. This is caused by changes in velocity and turbulence, and is considered minor when compared to major losses caused by friction.
2. How does sudden expansion affect fluid flow?
Sudden expansion causes the fluid to accelerate and the pressure to decrease momentarily. This can lead to turbulence and vortices, which can increase the friction and cause energy losses. However, these losses are typically small and considered "minor."
3. What factors can affect the magnitude of minor losses in sudden expansion?
The magnitude of minor losses in sudden expansion can be affected by the suddenness of the expansion, the ratio of the pipe diameters, and the properties of the fluid, including its density and viscosity. The geometry and roughness of the expansion can also play a role.
4. Can minor losses be avoided in sudden expansion?
While minor losses cannot be completely avoided, they can be reduced by gradually expanding the pipe or channel, using smooth and streamlined geometries, and controlling the fluid's velocity. Proper design and construction can also help minimize minor losses.
5. How are minor losses calculated in sudden expansion?
Minor losses in sudden expansion are typically calculated using empirical equations or experimental data. These equations take into account factors such as the expansion ratio, Reynolds number, and friction factor to estimate the magnitude of minor losses. However, it is important to note that these calculations are approximations and may not accurately reflect actual conditions.
Similar threads
-
Introductory Physics Homework Help
- Replies
- 12
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 3
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 11
- Views
- 691
-
Introductory Physics Homework Help
- Replies
- 3
- Views
- 127
-
Introductory Physics Homework Help
- Replies
- 33
- Views
- 3K
-
Introductory Physics Homework Help
- Replies
- 7
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 1
- Views
- 439
-
Introductory Physics Homework Help
- Replies
- 8
- Views
- 655
-
Introductory Physics Homework Help
- Replies
- 9
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 9
- Views
- 1K
Share: