James1238765
- 120
- 8
1. Random numerical ##g_{ij}## will generate valid ##T_{ij}##, with matter everywhere:

Thus, the difficulty is in generating the black vacuum (zeros), instead of the (white) matter.
2. Combinatorially, we consider a 2x2x2 universe grid, with only 2 matter states (matter ON, and matter OF):

The major difficulty is in generating any (black) vacuum at all in any subsquare. But supposing we have found a solution that turns off any subsquare:

By symmetry of the cartesian dimensional axis, we can deduce the correct ##g_{ij}## codes to turn off any other single square configuration on the grid. Thus, knowing just 1 single-black-square solution can generate all other single-black-square solutions.
Similarly, know 2 distinct solutions that turns off 2 areas of the grid:
 and
and

allows us by symmetry to deduce the ##g_{ij}## numbers that will turn off any 2-black-squares on the grid.
Further, knowing 2 distinct solutions that turns off 3 areas of the grid:
 and
and

enables us by symmetry to deduce the ##g_{ij}## numbers that will turn off any 3-black-squares on the grid.
Then, knowing 4 distinct solutions that turns off 4 areas of the grid:
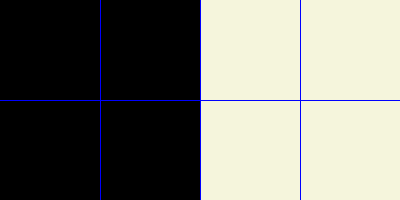
 (file limit reached)
(file limit reached)
allows us by symmetry to turn off any 4-black-squares on the grid.
There are 2 distinct solutions for 5-black-subsquares (ie. 3-white-subsquares).
There are 2 distinct solutions for 6-black-subsquares (ie. 2-white-subsquares).
There is 1 distinct solution for 7-black-subsquares (ie. 1-white-subsquares).
There is 1 distinct trivial solution for 8-black-subsquares (zero ##g_{ij}##).
Not counting the trivial solutions for all-white and all-black configurations, there are ##2+2+4+2+2=10## configuration solutions that must be discovered before we are masters of this universe, ie. are able to generate any of the ##2^8=256## possible matter states, and to evolve any sequence of matter states on this grid, eg:

3. The unfortunate case of the Kerr solution is that it generates 1 single-white-square at the center of a 3x3 grid, for which no other solution can be deduced by symmetry.
Thus, the difficulty is in generating the black vacuum (zeros), instead of the (white) matter.
2. Combinatorially, we consider a 2x2x2 universe grid, with only 2 matter states (matter ON, and matter OF):
The major difficulty is in generating any (black) vacuum at all in any subsquare. But supposing we have found a solution that turns off any subsquare:
By symmetry of the cartesian dimensional axis, we can deduce the correct ##g_{ij}## codes to turn off any other single square configuration on the grid. Thus, knowing just 1 single-black-square solution can generate all other single-black-square solutions.
Similarly, know 2 distinct solutions that turns off 2 areas of the grid:
allows us by symmetry to deduce the ##g_{ij}## numbers that will turn off any 2-black-squares on the grid.
Further, knowing 2 distinct solutions that turns off 3 areas of the grid:
enables us by symmetry to deduce the ##g_{ij}## numbers that will turn off any 3-black-squares on the grid.
Then, knowing 4 distinct solutions that turns off 4 areas of the grid:
allows us by symmetry to turn off any 4-black-squares on the grid.
There are 2 distinct solutions for 5-black-subsquares (ie. 3-white-subsquares).
There are 2 distinct solutions for 6-black-subsquares (ie. 2-white-subsquares).
There is 1 distinct solution for 7-black-subsquares (ie. 1-white-subsquares).
There is 1 distinct trivial solution for 8-black-subsquares (zero ##g_{ij}##).
Not counting the trivial solutions for all-white and all-black configurations, there are ##2+2+4+2+2=10## configuration solutions that must be discovered before we are masters of this universe, ie. are able to generate any of the ##2^8=256## possible matter states, and to evolve any sequence of matter states on this grid, eg:
3. The unfortunate case of the Kerr solution is that it generates 1 single-white-square at the center of a 3x3 grid, for which no other solution can be deduced by symmetry.