Moment of Inertia for a uniform wire

[SalsaOnMyTaco]

Homework Statement

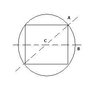
A flat object shown here consists of a circle and square made of heavy, uniform wire and welded together at the corners of the square. The mass of the circle is M. The mass of the square is m and its side has a length d. To find the objects moment of inertia about Axis A:
a)Find Moment of inertia of the square about Axis B in its plane.
- I=1/4 md²

b)Find Moment of inertia of the circle about the axis perpendicular to its plane at its center C.
- I came up wit I=Mr² (Not sure if its right?)

c)Use the perpendicular axis theorem to find the moment of inertia of the square about this same perpendicular axis.

d)Add to get the total moment of inertia about this Axis.

e)Use the perpendicular axis theorem again to get the moment of inertia about Axis A.

Homework Equations

I=I_CM + Mh²

I_Z=I_X + I_Y (not sure how this theorem works)

 

[SalsaOnMyTaco]

Actually I think I figured out B.
Iz=Ix+Iy
By symmetry Ix=Iy

So
2Ix=Iz Iz=Md^2/4
Ix=1/2Iz

Iz=md^2/8

Is this correct?