Moment of Inertia Homework: Parts C & D

[athrun200]

Homework Statement

part c and part d

And the ans.
a.)140
b.)130/21
c.)6.92M
d.)150M/7

Homework Equations

The Attempt at a Solution

It seems the ans is wrong, I am not sure.
Can you help me?

 

[cupid.callin]

the density you used is defined from the lighter end and you have to find I about heavier end.

you may take the dx element at distance x from heavy end and then use (10-x) in the equation of density

 

[gneill]

The parallel axis theorem works fine for objects with constant density. This object doesn't have constant density -- the density varies from end to end. Therefore there will be a light end and a heavy end. If you grab the rod by the light end and swing the heavy end around, you'll find a lot more angular inertia than if you grab the rod by the heavy end and swing the light end around.

So, see if you can set up your integral to directly find the moment of inertia about the heavy end.

 

[athrun200]

the density you used is defined from the lighter end and you have to find I about heavier end.

you may take the dx element at distance x from heavy end and then use (10-x) in the equation of density

Is it a rule that I must start from heavy end?

Why it is wrong to start from light end?

 

[gneill]

Is it a rule that I must start from heavy end?

Why it is wrong to start from light end?

It's not a rule, and it's not wrong to start at the light end. You may start anywhere you wish! But note that the problem is asking for the moment of inertia about the heavy end. Therefore, in the the calculation of the moment of inertia, the radial distances of the mass elements must be with respect to the heavy end. And be sure that the density at that distance from the heavy end is the correct density for that position along the rod.

 

[athrun200]

It's not a rule, and it's not wrong to start at the light end. You may start anywhere you wish! But note that the problem is asking for the moment of inertia about the heavy end. Therefore, in the the calculation of the moment of inertia, the radial distances of the mass elements must be with respect to the heavy end. And be sure that the density at that distance from the heavy end is the correct density for that position along the rod.

Oh! Sorry for my carelessness, I didn't read the question carefully.
I have solved part d, but part c is still very complicated.

The result I obtained is so ugly that I don't want to write it out.
But I have check it and it is wrong.

So what's wrong with my work this time?

 

[gneill]

Suppose you break the integral into two. The first runs from x=0 to x= x_cm, the second from x_cm to 10. The density function remains as 2x + 4 for any value of x, so leave it alone. What is the distance from x_cm to the mass element in each case?

 

[athrun200]

Suppose you break the integral into two. The first runs from x=0 to x= x_cm, the second from x_cm to 10. The density function remains as 2x + 4 for any value of x, so leave it alone. What is the distance from x_cm to the mass element in each case?

I am so sorry that I don't understand.
Can you explain it more clearly?:shy:

 

[gneill]

I am so sorry that I don't understand.
Can you explain it more clearly?:shy:

x is the position along the rod from the LHS. For the region to the left of the center of mass, the distance from the center of mass to x is x_cm - x. To the right of the center of mass, the distance is x - x_cm. The density at point x remains \rho (x) = 2 x + 4, since here x is always with respect to the light end of the rod.

 

[athrun200]

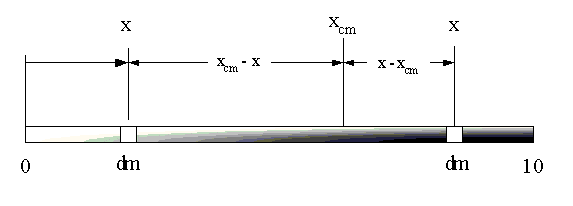
x is the position along the rod from the LHS. For the region to the left of the center of mass, the distance from the center of mass to x is x_cm - x. To the right of the center of mass, the distance is x - x_cm. The density at point x remains \rho (x) = 2 x + 4, since here x is always with respect to the light end of the rod.

Do you mean this?
I have just finished half of the integral.

 

[athrun200]

Oh! It works and I get the answer!

But can you explain what's wrong with my method?
Why I can't set the center of mass as the orgin?

 

[athrun200]

Work in #6 turns out to be correct, I just type it wrongly in my calculator.

By the way, how to generate the picture in #9?
What software are you using?

 

[gneill]

Oh! It works and I get the answer!

But can you explain what's wrong with my method?
Why I can't set the center of mass as the orgin?

You can set the center of mass at the origin if you translate the density equation accordingly for each section of the rod. Personally I tend to find it easier to leave the density function alone and work out the required distances as functions of the same x.

 

[gneill]

Work in #6 turns out to be correct, I just type it wrongly in my calculator.

By the way, how to generate the picture in #9?
What software are you using?

I use Visio to draw the pictures, then paste it into MS Paint to save it as a .gif type file.