Moment of Inertia: Object w/ Rod & Sphere

AI Thread Summary
The discussion focuses on calculating the moment of inertia for a combined object consisting of a rod and a sphere. The user initially applied the formulas for the moment of inertia of the rod and sphere but made an error in the application of the parallel axis theorem. Specifically, the user incorrectly included a linear distance instead of the squared distance in the second term for the sphere's moment of inertia. After recognizing the mistake, the user acknowledges the need to correct the calculation to arrive at the accurate moment of inertia. The conversation emphasizes the importance of careful application of physics equations in solving such problems.
cp255
Messages
54
Reaction score
0

Homework Statement



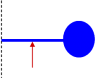
An object is formed by attaching a uniform, thin rod with a mass of mr = 6.91 kg and length L = 4.88 m to a uniform sphere with mass ms = 34.55 kg and radius R = 1.22 m. Note ms = 5mr and L = 4R.

What is the moment of inertia of the object about an axis at the left end of the rod?

attachment.php?attachmentid=56284&stc=1&d=1362266421.png


Homework Equations


I came up with these equations...
I_rod = (1/3) * mr * L^2
I_sphere = (2/5) * ms * R^2 + ms * (L + R)

The Attempt at a Solution



I think that the moment of inertia for the system is equal to the sum of I_rod and I_sphere. So I simply plugged in the relevant variables and got the answer of 286.177 kg-m^2 which is wrong. Are the equations above correct?
 

Attachments

  • momentofinertia1new.png
    momentofinertia1new.png
    947 bytes · Views: 3,055
Physics news on Phys.org
cp255 said:
I_sphere = (2/5) * ms * R^2 + ms * (L + R)
That second term, from the parallel axis theorem, should have the distance squared.
 
Thanks. That was stupid of me. I did the problem twice and made the same mistake twice.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Correct Use of the Parallel Axis Theorem for Moment of Inertia
Replies
2
Views
2K
Parallel Axis Theorem Not Working
Replies
28
Views
1K
Finding the angular velocity of a pendulum
Replies
3
Views
905
Moment of inertia of T bar about 3 axes
Replies
21
Views
2K
Moment of inertia of a disk about an axis not passing through its CoM
Replies
11
Views
3K
Two objects joined by a rectilinear cable rotating
Replies
8
Views
858
Moment of Inertia of this combined system?
Replies
3
Views
2K
Moment of inertia of a disc using rods as differential elements
Replies
8
Views
2K
Determine the moment of inertia of a bar and disk assembly
Replies
3
Views
3K
Moment of inertia of a rod bent into a square
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top