Moment of Inertia of an Ammonium Molecule

[Rafimah]

Homework Statement

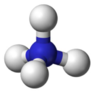
The ammonium ion NH4+ has the shape of a regular tetrahedron. The Nitrogen
atom (blue sphere) is at the center of the tetrahedron and the 4 Hydrogen atoms
are located at the vertices at equal distances L from the center (about 1 Å). Denote
the mass of the hydrogen atoms by Mh and that of the nitrogen atom by Mn.
a. What is the moment of inertia I0 of NH4+ for rotation along any of the 4
axes that passes through the central nitrogen atom and one of the 4
hydrogen atoms? Express your answer in terms of Mh, Mn and L. (Hint:
The central angle between the lines to any two vertices of a perfect
tetrahedron is acos(-1/3) or approximately 110 deg.)

b. Derive an expression for the moment of inertia tensor I for the ammonium
ion. Can you show that I0 is one of the principal moments of I and that in
fact all principal moments must equal I0 (The ammonium is a spherical
top)?

Homework Equations

To solve part a, I simply use $$ \sum{m_h r^2} $$ . I reasoned that for part b, I should do the same about two axes perpendicular to one running through one of the hydrogen atoms and the central atoms. I figured these two moments of inertia should be degenerate based on the symmetry and I solved, getting $$m_h L^2 (1+3 sin(20)^2) $$. However, I don't think this can be simplified to be equivalent to my answer for part a, $$ 3 m_h L^2 cos(70)^2 $$. Am I doing something wrong here? Also, do I need to show that the off diagonal elements are zero in this tensor or can I assume that if I find the three moments of inertia are equivalent? Also, I assumed that the origin here would be the coordinate of the central atom, is that acceptable?

The Attempt at a Solution

See above

 

[kuruman]

The problem is asking you to find the moment of inertia tensor. That is a 3×3 symmetric matrix. First you have to write down the positions of all the masses using the coordinate system that is given to you and then you need to use the formulas for the diagonal and off diagonal elements of the inertia tensor. It is acceptable to use the central atom as the origin. Yes, you need to verify that the off diagonal elements are zero.

 

[Rafimah]

I think I was doing this for the diagonal parts of the tensor, the formula gives the radial distance from the axis as the term to multiply the mass of the particle, which is what I believe I found for each axis.

 

[kuruman]

I figured these two moments of inertia should be degenerate based on the symmetry ...

What is the symmetry argument that you invoked to argue that the moments of inertia about the perpendicular axes are equal?

and I solved, getting

$$m_hL^2(1+3 \sin(20)^2)$$​

What is it that you solved? Is this expression for the perpendicular moment of inertia?
This doesn't look right. Say you put one of the perpendicular axes, the x-axis, in a plane containing two hydrogen atoms and the central atom and call that the xz-plane. The expression to use is$$I_{xx}=m_h\sum_k \left( y_k^2+z_k^2 \right)$$ One H-atom in the xz-plane is at $r_1=(0,0,L)$ and the other at $r_2=(L \cos20^o,0,- L \sin20^o)$. However, the remaining two off-the-plane H-atoms are at $r_3=(x_3,y_3,- L \sin20^o)$ and $r_4=(x_4,y_4,- L \sin20^o)$. The x-components of these do not contribute to $I_{xx}$ but the y-components are non-zero. Therefore they do contribute and you have to find what they are.