Moment of Inertia of something that rotates

[Lambda96]

Homework Statement

Calculate the moment of inertia of the system

Relevant Equations

none

Hi,

unfortunately, I am completely confused about the task

It is about the task part a

I have now defined the two rotations as follows:

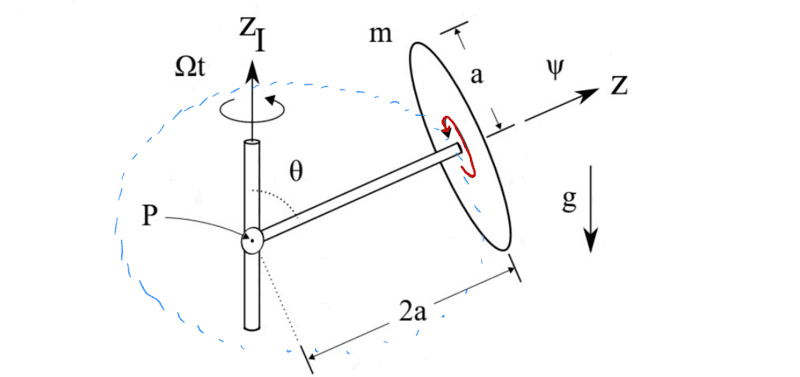
The thin disc rotates around the $z$ axis, red in the picture, and then the rod to which the disc is attached rotates around the $z_I$ axis, in the picture I have drawn the circular path with blue dots.

I then assumed that $I_z^P$ is the red moment of inertia and $I^P$ is the blue moment of inertia.

$I_z^P$ is therefore $I_z^P=\frac{1}{2}ma^2$

The moment of inertia $I^P$ is then a bit more difficult, the thin disc is too close to the axis, $z_I$ so I cannot approximate the disc as a point mass. I probably have to use the parallel axis theorem here, right?

Is my interpretation of the moment of inertia correct or have I already made a mistake here?

 

[TSny]

The thin disc rotates around the $z$ axis, red in the picture, and then the rod to which the disc is attached rotates around the $z_I$ axis, in the picture I have drawn the circular path with blue dots.

I then assumed that $I_z^P$ is the red moment of inertia and $I^P$ is the blue moment of inertia.

$I_z^P$ is therefore $I_z^P=\frac{1}{2}ma^2$

This looks right for $I_z^P$.

The moment of inertia $I^P$ is then a bit more difficult, the thin disc is too close to the axis, $z_I$ so I cannot approximate the disc as a point mass. I probably have to use the parallel axis theorem here, right?

Is my interpretation of the moment of inertia correct or have I already made a mistake here?

From the statement of the problem, $I^P = I_x^P = I_y^P$ where $x$ and $y$ refer to $X$ and $Y$ axes that are perpendicular to the Z-axis and the origin of the $XYZ$ set of axes is located at point $P$.

I've attempted to indicate the $X$ and $Y$ axes at some instant of time in the figure above. The imaginary dotted ellipse represents the orientation of the spinning disk. The $X$ and $Y$ axes lie in the plane of the dotted ellipse. I believe that the $XYZ$ axes are "body-fixed" axes that rotate with the spinning disk. $I_x^P$ is the moment of inertia of the system about the $X$-axis. You can use the parallel axis theorem to determine $I_x^P$ and $I_y^P$.

 

[Lambda96]

Thank you TSny for your help

The moment of inertia $I_x^P=I_y^P=I^P$ or rather how this is oriented in space has confused me the most. I have now proceeded as follows, that moment of inertia $I^{CM}$ is defined as follows, $I^{CM}=\frac{1}{4}ma^2$ and the parallel axis theorem is $I^{CM}+md^2$ so then the moment of inertia for $I_x^P=I_y^P=I^P$ is as follows.

$$I_x^P=I_y^P=I^P=\frac{1}{4}ma^2+4a^2$$

Thus, the moments of inertia are

$$I_z^P=\frac{1}{2}ma^2$$
$$I_x^P=I_y^P=I^P=\frac{1}{4}ma^2+4a^2$$

One more question @TSny, what program did you use to make the drawing?

 

[TSny]

Thus, the moments of inertia are

$$I_z^P=\frac{1}{2}ma^2$$
$$I_x^P=I_y^P=I^P=\frac{1}{4}ma^2+4a^2$$

Looks good except for a missing factor of $m$ in one of the terms.

One more question @TSny, what program did you use to make the drawing?

I used Microsoft Paint.

 

[Lambda96]

Thanks for your help and for answering my question TSny

Right, unfortunately I had forgotten to include the mass

Regarding task b and c, I proceeded as follows.

$\textbf{task b}$
In the lecture notes we defined $\omega_x$, $\omega_y$ and $\omega_z$ as follows

$$\omega_x=\dot{\phi}sin\theta sin\psi + \dot{\theta} cos\psi$$
$$\omega_y=\dot{\phi}sin\theta cos\psi - \dot{\theta} sin\psi$$
$$\omega_z=\dot{\phi}cos\theta + \dot{\psi}$$

The above formula match the angle, in the task, but instead of $\dot{\phi}$ I have to use $\Omega$, so the individual angular velocities are.

$$\omega_x=\Omega sin\theta sin\psi + \dot{\theta} cos\psi$$
$$\omega_y=\Omega sin\theta cos\psi - \dot{\theta} sin\psi$$
$$\omega_z=\Omega cos\theta + \dot{\psi}$$

$\textbf{task c}$

We have defined the rotational energy as follows:

$$\frac{1}{2}(I_x \omega_x^2+I_y \omega_y^2+I_z \omega_z^2)$$

Since the following applies, $I^P=I_x^P=I_y^P$, the rotational energy for this task can be written as follows

$$\frac{1}{2}(I^P(\omega_x^2+\omega_y^2)+I_z^P \omega_z^2)$$

The Lagrange Equation is thus

$$L=\frac{1}{2}I^P(\Omega^2 sin^2 \theta+\dot{\theta^2})+\frac{1}{2}I_z^P(\Omega cos\theta + \dot{\psi^2})+2 \ a \ m \ g \ cos\theta$$

I'm just a bit confused now, because in the task the Lagrange Equations were defined as follows $L(\psi , \theta , \dot{\psi} , \dot{\theta})$ but in my equation $\Omega$ still appears, have I miscalculated or did the creator of the task simply forget that?

 

[TSny]

Everything looks good until you wrote the Lagrangian

The Lagrange Equation is thus

$$L=\frac{1}{2}I^P(\Omega^2 sin^2 \theta+\dot{\theta^2})+\frac{1}{2}I_z^P(\Omega cos\theta + \dot{\psi^2})+2 \ a \ m \ g \ cos\theta$$

The square on $\dot \psi$ is misplaced. It should be outside the parentheses.
I believe the $+$ in front of the potential energy should be $-$ .
(These could just be typos.)

I'm just a bit confused now, because in the task the Lagrange Equations were defined as follows $L(\psi , \theta , \dot{\psi} , \dot{\theta})$ but in my equation $\Omega$ still appears, have I miscalculated or did the creator of the task simply forget that?

I agree. For this problem, $\theta$ and $\psi$ are the generalized coordinates and $L$ is a function of $\theta$, $\dot \theta$, and $\dot \psi$.
$\Omega$ is just a parameter and is treated as a constant when deriving the equations of motion.

 

[Lambda96]

Thanks again TSny for your help

That's right, unfortunately it ended up in the wrong place when I entered it with latex.

Unfortunately the task goes even further

Unfortunately, I am not sure if I am solving task e correctly.

I have now started with $\psi$, as I will have to insert this into the equation for $\theta$ later.

For the Euler Lagrange equation I proceeded as follows

$$\frac{\partial L}{\partial \psi}=0$$
$$\frac{\partial L}{\partial \dot{\psi}}=2\Omega cos\theta+2\dot{\psi}$$

Now I'm not quite sure, unfortunately, I have to form the time derivative of $\frac{\partial L}{\partial \dot{\psi}}$, i.e. $-\frac{d}{dt}(2\Omega cos\theta+2\dot{\psi})$. Unfortunately, I am not sure how to deal with the terms $\Omega^2$ and $\theta$. These are also time-dependent and I have also taken these into account accordingly and obtained the following.

$$-2\Omega cos(\theta)+2\dot{\theta}sin\theta-2\ddot{\psi}$$

I have now solved this differential equation for $\psi$.

$$\psi(t)=-\frac{1}{2} \dot{\Omega}cos\theta t^2+\frac{1}{2}\Omega \dot{\theta}sin\theta t^2+c_1t+c_2$$

Is that right?

 

[TSny]

Unfortunately the task goes even further

Sneaky

$$\frac{\partial L}{\partial \dot{\psi}}=2\Omega cos\theta+2\dot{\psi}$$

How did you get this starting from
$$L=\frac{1}{2}I^P(\Omega^2 \sin^2 \theta+\dot{\theta}^2)+\frac{1}{2}I_z^P(\Omega \cos\theta + \dot{\psi})^2-2 a m g \cos\theta \, \rm?$$

Now I'm not quite sure, unfortunately, I have to form the time derivative of $\frac{\partial L}{\partial \dot{\psi}}$, i.e. $-\frac{d}{dt}(2\Omega cos\theta+2\dot{\psi})$. Unfortunately, I am not sure how to deal with the terms $\Omega^2$ and $\theta$. These are also time-dependent and I have also taken these into account accordingly and obtained the following.

$$-2\Omega cos(\theta)+2\dot{\theta}sin\theta-2\ddot{\psi}$$

Did you mean to set this equal to zero?

I have now solved this differential equation for $\psi$.

$$\psi(t)=-\frac{1}{2} \dot{\Omega}cos\theta t^2+\frac{1}{2}\Omega \dot{\theta}sin\theta t^2+c_1t+c_2$$

Is that right?

No, you did not solve your differential equation for $\psi$ correctly. $\theta$ and $\dot \theta$ are unknown functions of time in your differential equation. So, you cannot solve it as you did.

Before going any further with part (e), I think it would be good to look at what you did for part (d).

 

[Lambda96]

Sorry that I'm only posting the rest of the problem now, but since it depends on problem parts a,b and c, I only posted this one at first and hoped that I would be able to do the rest, which is unfortunately not the case.

For task d I simply formed the Euler Lagrange equation, so $\frac{\partial L}{\partial \psi}-\frac{d}{dt}\frac{\partial L}{\partial \dot{\psi}}=0$ the Lagrange equation is

$$L=\frac{1}{2}I^P(\Omega^2 sin^2\theta + \dot{\theta}^2) + \frac{1}{2}I_x^P(\Omega cos\theta + \dot{\psi})^2 -2 \ a \ m \ g \ cos\theta$$

However, for the calculation I only need to calculate the term $\frac{1}{2}I_x^P(\Omega cos\theta + \dot{\psi})^2$, since there is no $\psi$ or $\dot{\psi}$ in the other terms

However, since there is no $\psi$ in the expression, $\frac{\partial L}{\partial \psi}=0$ which means that the following holds $-\frac{d}{dt}\frac{\partial L}{\partial \dot{\psi}}=0$ the expression $\frac{\partial L}{\partial \dot{\psi}}$ would be constant in time after all, so.

$$\frac{1}{2}I_x^P(2\Omega cos\theta + 2\dot{\psi})=A$$

This would then mean that the angular momentum would be constant with respect to the $z$ axis.

 

[BvU]

Keep going ....

Tip: use ##\cos## and ##\sin## to get $\cos$ and $\sin$ instead of $cos$ and $sin$ -- it also gives better spacing

$\$

 

[TSny]

Sorry that I'm only posting the rest of the problem now, but since it depends on problem parts a,b and c, I only posted this one at first and hoped that I would be able to do the rest, which is unfortunately not the case.

That's fine.

For task d I simply formed the Euler Lagrange equation, so $\frac{\partial L}{\partial \psi}-\frac{d}{dt}\frac{\partial L}{\partial \dot{\psi}}=0$ the Lagrange equation is

$$L=\frac{1}{2}I^P(\Omega^2 sin^2\theta + \dot{\theta}^2) + \frac{1}{2}I_x^P(\Omega cos\theta + \dot{\psi})^2 -2 \ a \ m \ g \ cos\theta$$

However, for the calculation I only need to calculate the term $\frac{1}{2}I_x^P(\Omega cos\theta + \dot{\psi})^2$, since there is no $\psi$ or $\dot{\psi}$ in the other terms

However, since there is no $\psi$ in the expression, $\frac{\partial L}{\partial \psi}=0$ which means that the following holds $-\frac{d}{dt}\frac{\partial L}{\partial \dot{\psi}}=0$ the expression $\frac{\partial L}{\partial \dot{\psi}}$ would be constant in time after all, so.

$$\frac{1}{2}I_x^P(2\Omega cos\theta + 2\dot{\psi})=A$$

This would then mean that the angular momentum would be constant with respect to the $z$ axis.

Yes, that's all very good. (Of course, you can cancel the 2.) The constant $A$ would be determined from this equation using the initial conditions on $\theta$ and $\dot\psi$. Note that you can think of this angular momentum expression as a differential equation for $\dot \psi$. There is no need to get a differential equation for $\ddot \psi$. At this point, you can't solve the angular momentum equation for $\psi$ since it involves the unknown function $\theta(t)$.

When you go on to part (e) to derive the differential equation for $\theta$, you can make use of
$I_x^P(\Omega cos\theta + \dot{\psi})=A$. So, what do you get for part (e)?

[Edit: I believe there is a typo in your Lagrangian. Where you wrote $I_x^P$, it should be $I_z^P$. You had this right in post #5.]

 

[Lambda96]

Many thanks TSny for your help

Also, many thanks to BvU with the tip for sin and cos

@TSny, you are right, I used the wrong index for the moment of inertia, it should be $I_z^P$

I asked my lecturer again, he said I only have to derive the equation of motion, but not solve it. As you wrote correctly, you can use the expression in problem d to derive for $\dot{\theta}$, unfortunately that was a typo in the original problem. It should read Use the results in d)

The Euler Lagrange equation for $\dot{\theta}$ is as follows

$$I_z^P \Omega^2 \sin\theta \cos\theta -I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \Omega \sin\theta \dot{\psi}+2amg \cos\theta -2\ddot{\theta}=0$$

I then proceeded as follows, I first put $2\ddot{\theta}$ on the other side of the equation.

$$I_z^P \Omega^2 \sin\theta \cos\theta -I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \Omega \sin\theta \dot{\psi}+2amg \cos\theta =2\ddot{\theta}$$

Now simply solve the result from task d for $\dot{\psi}$ which gives the following $\dot{\psi}=\frac{A}{I_z^P}-\Omega \cos\theta$ and insert into the equation above.

$\\$

$$I_z^P \Omega^2 \sin\theta \cos\theta -I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \Omega \sin\theta (\frac{A}{I_z^P}-\Omega \cos\theta) +2amg \cos\theta =2\ddot{\theta}$$
$$I_z^P \Omega^2 \sin\theta \cos\theta -I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \frac{A}{I_z^P}\Omega \sin\theta -\Omega^2 \cos\theta \sin\theta +2amg \cos\theta =2\ddot{\theta}$$
$$I_z^P \Omega^2 \sin\theta \cos\theta -2I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \frac{A}{I_z^P}\Omega \sin\theta +2amg \cos\theta =2\ddot{\theta}$$
$$\frac{I_z^P}{2} \Omega^2 \sin\theta \cos\theta -I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \frac{A}{2I_z^P}\Omega \sin\theta +amg \cos\theta =\ddot{\theta}$$

 

[TSny]

The Euler Lagrange equation for $\dot{\theta}$ is as follows

$$I_z^P \Omega^2 \sin\theta \cos\theta -I_x^P \Omega^2 \sin\theta \cos\theta-I_x^P \Omega \sin\theta \dot{\psi}+2amg \cos\theta -2\ddot{\theta}=0$$

Some things don't look right here:

Do you have $I_z^P$ and $I_x^P$ interchanged?

Your last term on the left side is $-2\ddot\theta$. Does this term have the same dimensions as the other terms in the equation? Should the factor of 2 be there?

EDIT: Also, check the next to last term on the left side where you have $+2amg \cos\theta$. When working out $\frac{\partial L}{\partial \theta}$, you should have taken the derivative of $-2amg \cos\theta$ with respect to $\theta$. This doesn't yield $+2amg \cos\theta$.
_________________________________________
Here's something that might save you some time. The two middle terms on the left side (with $I_x^P$ replaced by $I_z^P$) will combine to $$-I_z^P \left( \Omega \cos\theta + \dot \psi \right) \Omega \sin\theta = -A \Omega \sin \theta$$

 

[Lambda96]

Thank you TSny for your help

You are absolutely right, unfortunately there were some sign errors and notation errors in my calculation, I think I am still not fully recovered from my cold.

I ran the calculation again and got the following

$$\ddot{\theta}=\frac{1}{2}I^P \Omega^2 \sin\theta \cos\theta - \frac{1}{2} \Omega \sin\theta A - amg \sin\theta$$

unfortunately I cannot find the error in the calculation $\ddot{\theta}$, I calculated it with the help of the Euler Larange equation, i.e. the term $\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}$ and the only term in $L$ was the term $\dot{\theta^2}$ then I calculated

$$\frac{\partial L}{\partial \dot{\theta}}=2\dot{\theta}$$
$$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}=2\ddot{\theta}$$

Did I miss something in the calculation?

Regarding task f, do I simply have to put $\theta=0$ in the result for task d now and after $\psi$? Unfortunately, I am not quite sure what exactly is meant by the following formulation?

Derive a condition on the initial angular speed $\dot{\psi}(0)$ of the disc, for the linearized motion being stable around $\theta= 0$.

 

[TSny]

I ran the calculation again and got the following

$$\ddot{\theta}=\frac{1}{2}I^P \Omega^2 \sin\theta \cos\theta - \frac{1}{2} \Omega \sin\theta A - amg \sin\theta$$

unfortunately I cannot find the error in the calculation $\ddot{\theta}$, I calculated it with the help of the Euler Larange equation, i.e. the term $\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}$ and the only term in $L$ was the term $\dot{\theta^2}$ then I calculated

$$\frac{\partial L}{\partial \dot{\theta}}=2\dot{\theta}$$
$$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}=2\ddot{\theta}$$

Did I miss something in the calculation?

In the Lagrangian, $\dot\theta^2$ is multiplied by $\frac 1 2 I^P$. So, $\large \frac{\partial L}{\partial \dot \theta} = \frac{\partial }{ \partial \dot \theta} \left(\frac{1}{2}I^P \dot \theta^2\right)$.

Also, check the sign of the $amg\sin\theta$ term.

Regarding task f, do I simply have to put $\theta=0$ in the result for task d now and after $\psi$? Unfortunately, I am not quite sure what exactly is meant by the following formulation?

Derive a condition on the initial angular speed $\dot{\psi}(0)$ of the disc, for the linearized motion being stable around $\theta= 0$.

Once you get the equation of motion (differential equation) involving $\ddot \theta$, you want to "linearize" the equation under the assumption that $\theta$ is small. This means to Taylor expand $\sin \theta$ and $\cos \theta$ and drop all terms in the equation of motion that contain powers of $\theta$ greater than or equal to 2. Then, you should be able to see the nature of the solutions of the linearized equation and investigate how the stability of the solutions depends on $\dot \psi(0)$.

Hope you get over your cold soon.

 

[Lambda96]

Hope you get over your cold soon.

Thank you, fortunately I'm feeling a little better now

Thanks for your help TSny with the task, I would have been really lost without you I wish you a Merry Christmas