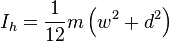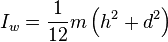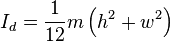Moment of intertia of a cuboid

[Stickybees]

Simple question but I've never been through the proofs to know what I'm plugging into.
Are these components of the cuboid and can they just be added together for the total moment of inertia?

Thanks!

 

[Electric Red]

It is very important that you check every step that I take, try to understand what I do.

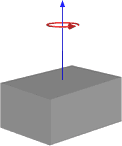
Think of a cuboid like this one:

The shape with sides A and B is a quarter of the whole shape with sides C and D. The column with sides a and b is very narrow, where a and b tend to go to zero.

The total moment of intertia is given by: I = \sum\limits_{i=1}^n m_ir_i^2

Calculating the mass of the narrow column: m=ρabh
(assuming the mass-desnsity is homogenous, we call it ρ)

The distance from the axis of rotation:
r=\sqrt{a^2+b^2}

So

I=ρh\int_a^A\int_b^B(a^2+b^2)da db<br /> =hρ\int_a^A\frac{1}{3}B^3+Ba^2da<br /> =hρ[\frac{1}{3}B^3A+\frac{1}{3}BA^3]<br /> =\frac{1}{3}hρBA(B^2+A^2)<br />But we do not have one of those blocks, but four of them, so multiply by four gives:

I=\frac{4}{3}hρBA(B^2+A^2)

From the image on the beginning, we can conclude that A=C/2, and that B=D/2,
putting this into the last equation gives:

I=\frac{1}{12}hρCD(C^2+D^2)

The mass of such a cuboid is given by

m=ρABh

so

I=\frac{1}{12}m(C^2+D^2)

If you were to replace the C and D with w, d or h, you will get your answer.

 

[SteamKing]

It's not clear what the OP is talking about when he mentions the 'total moment of inertia' of the cuboid.

The moment of inertia of anybody depends on the axis of rotation. For example, the MOI of a long, slender rod is a minimum when the rod is rotated about an axis which runs along the length of the rod and through the center of the cross section. If the rod is rotated about an axis which is perpendicular to the rod, then the MOI can be greater.