Clutch306
- 7
- 0
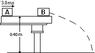
In the attached figure, block A of mass 2.0kg slides on a horizontal frictionless table with velocity of 3.0m/s and collides with block B of mass 3.0kg initially at rest on the edge of the table. Block B moves with a horizontal velocity of 2.4m/s, just after the collision.
(a) Use conversation of momentum to find the velocity of Block A, after the collision
(b) Is the collision elastic? (Hint: Verify K.E. of the block before & after collision)
(c) What is the kinetic energy of block B, just before it strikes the floor 0.40m below the table's surface? (Hint use conservation of M.E.)
(a) Use conversation of momentum to find the velocity of Block A, after the collision
(b) Is the collision elastic? (Hint: Verify K.E. of the block before & after collision)
(c) What is the kinetic energy of block B, just before it strikes the floor 0.40m below the table's surface? (Hint use conservation of M.E.)