Rocket_Au
- 3
- 0
i need help getting started on a fluid mechanics problem, i am not looking for a worked solution just a nudge to get me started on the problem, i am rather stumped.
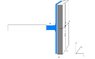
i need to determine the volume flow rate Q required to overcome the inertia of a homogenous rectangular block with weight N.
the block of d(x), w(y), h(z) stands at rest on the x-y plane, the fluid acts on the centroid of the block.
assume:
- negligable distance from nozzle to block
- steady flow
- incompressible fluid
the part of my memory that is trying to make it's way to the surface tells me to quantify the inertia(?) of the homogenous block at rest and calculate the amount of momentum required to tip the block from it's resting position.
based on other problems i have completed i don't expect to have any problems calculating the required flow rate to produce such a momentum.
it really seems as though i am missing a basic relationship/principle to get me started on the problem.
i need to determine the volume flow rate Q required to overcome the inertia of a homogenous rectangular block with weight N.
the block of d(x), w(y), h(z) stands at rest on the x-y plane, the fluid acts on the centroid of the block.
assume:
- negligable distance from nozzle to block
- steady flow
- incompressible fluid
the part of my memory that is trying to make it's way to the surface tells me to quantify the inertia(?) of the homogenous block at rest and calculate the amount of momentum required to tip the block from it's resting position.
based on other problems i have completed i don't expect to have any problems calculating the required flow rate to produce such a momentum.
it really seems as though i am missing a basic relationship/principle to get me started on the problem.
Attachments
Last edited: