Motion analysis of an accelerating wedge and a block

[NoahCygnus]

I don't understand the motion of an accelerating wedge and a block. I'd really appreciate if you make me understand the motion in both an inertial and a non inertial reference frame.

Here's a figure I have made, a0 is the acceleration on the wedge with respect to an inertial frame, towards right.

 

[zwierz]

Is $a_0$ given? If so then the mass M of the wedge is not needed

 

[NoahCygnus]

Is $a_0$ given? If so then the mass M of the wedge is not needed

Yes , a0 is towards right. I apologise, I made a mistake earlier by saying a0 is towards left.

 

[zwierz]

Let's start from inertial viewpoint. Write down the Newton Second Law for the briсk

 

[NoahCygnus]

Let's start from inertial viewpoint. Write down the Newton Second Law for the briсk

Let's take the angle of incline as θ. Applying Newton's Second Law to the block;
∑Fx = mgsinθ = ma (Where a is acceleration with respect to ground, which we take to be inertial.)
∑Fy = N - mgcosθ = 0 ⇔ N = mgcosθ

Am I correct?

 

[zwierz]

Stop! do not be so quickly. First we must write the Newton second Law in vector form: $m\boldsymbol a=m\boldsymbol g+\boldsymbol T$; here $\boldsymbol a$ is an acceleration of the brick relative to an inertial frame. This was the first step of the solution. Now you can expand this vector equality by any coordinate frame you want. Let's introduce a frame $Oxy$ such that $O$ is the highest angle of the wedge and the axis $OX$ goes down along the slope; Oy is directed upwards perpendicular to the slope.
Then $\boldsymbol T=T\boldsymbol e_y;$
$\boldsymbol g=..$
$\boldsymbol a=$
go on

 

[zwierz]

Let's take the angle of incline as θ. Applying Newton's Second Law to the block;
∑Fx = mgsinθ = ma (Where a is acceleration with respect to ground, which we take to be inertial.)
∑Fy = N - mgcosθ = 0 ⇔ N = mgcosθ

Am I correct?

no

 

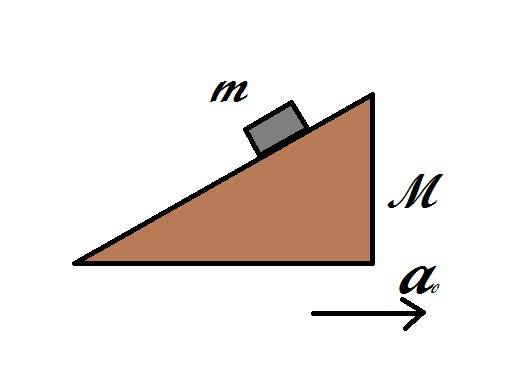
[NoahCygnus]

Stop! do not be so quickly. First we must write the Newton second Law in vector form: $m\boldsymbol a=m\boldsymbol g+\boldsymbol T$; here $\boldsymbol a$ is an acceleration of the brick relative to an inertial frame. This was the first step of the solution. Now you can expand this vector equality by any coordinate frame you want. Let's introduce a frame $Oxy$ such that $O$ is the highest angle of the wedge and the axis $OX$ goes down along the slope; Oy is directed upwards perpendicular to the slope.
Then $\boldsymbol T=T\boldsymbol e_y;$
$\boldsymbol g=..$
$\boldsymbol a=$
go on

no

Why not? Those are the only forces I see.

 

[jbriggs444]

Why not? Those are the only forces I see.

View attachment 205294
Let's take the angle of incline as θ. Applying Newton's Second Law to the block;
∑Fx = mgsinθ = ma (Where a is acceleration with respect to ground, which we take to be inertial.)
∑Fy = N - mgcosθ = 0 ⇔ N = mgcosθ

Am I correct?

Partly. You seem to be adopting a coordinate system where "x" is along an axis rotated θ up from the horizontal and where "y" is along the axis at right angles to that. [This coordinate system is notionally fixed in space. It does not move with the wedge]. Against that coordinate system, only g has any component along the x axis. We may immediately determine the x component of the acceleration of the block. You have done that and correctly computed $ma_x$ for the block.

You have not computed $m\vec{a}$ for the block.

You have not justified the claim that N = mg cos θ. Why should that be so?

 

[NoahCygnus]

Partly. You seem to be adopting a frame of reference where "x" is along an axis rotated θ up from the horizontal and where "y" is along the axis at right angles to that. [This coordinate system is notionally fixed in space. It does not move with the wedge]. Against that coordinate system, only g has any component along the x axis. We may immediately determine the x component of the acceleration of the block. You have done that and correctly computed $ma_x$ for the block.

You have not computed $m\vec{a}$ for the block.

You have not justified the claim that N = mg cos θ. Why should that be so?

Doesn't the block stay in contact with wedge through out the motion? Let's see, the wedge moves to right with acceleration a0, and at the same time, the block moves down with an acceleration of mgcosθ. I thought the normal force stayed same. I must admit, this motion is confusing me.

 

[jbriggs444]

Doesn't the block stay in contact with wedge through out the motion? Let's see, the wedge moves to right with acceleration a0, and at the same time, the block moves down with an acceleration of mgcosθ. I thought the normal force stayed same. I must admit, this motion is confusing me.

The normal force does not stay the same. The block does not move down with an acceleration mg cosθ (as it would if the normal force were zero).

Is $a_0$ given? Or is is something that you wish to compute?

 

[NoahCygnus]

Ah, yes, that makes sense. I am new to Newtonian mechanics, so I am likely to make mistakes. Can you tell me why normal force does not remain the same?

 

[jbriggs444]

Ah, yes, that makes sense. I am new to Newtonian mechanics, so I am likely to make mistakes. Can you tell me why normal force does not remain the same?

The wedge is accelerating (or is allowed to accelerate -- you still have not said which). If $\vec{A}$ is the acceleration of the wedge, what is A_y? If A_y is the acceleration of the wedge in the y direction, what is a_y -- the acceleration of the block in the y direction?

Write down a force balance for the block in the y direction. ∑F_y = ma_y

 

[NoahCygnus]

The wedge is accelerating (or is allowed to accelerate -- you still have not said which). If $\vec{A}$ is the acceleration of the wedge, what is A_y? If A_y is the acceleration of the wedge in the y direction, what is a_y -- the acceleration of the block in the y direction?

Write down a force balance for the block in the y direction. ∑F_y = ma_y

The wedge is accelerating towards right. Ay should be 0, as the wedge is not acceleration upward or downward. What do you mean by "Ay is the acceleration of the block"? Didn't you just say A is the acceleration on the wedge?

 

[jbriggs444]

The wedge is accelerating towards right. Ay should be 0

You rotated your coordinate axes. "right" has a component in the direction of negative y.

What do you mean by "Ay is the acceleration of the block"? Didn't you just say A is the acceleration on the wedge?

I editted that post a few times. It should read better now.

 

[NoahCygnus]

You rotated your coordinate axes. "right" has a component in the direction of negative y.

I editted that post a few times. It should read better now.

Do I have to choose the same coordinate system for the wedge that I chose for block? If I do so, the component of acceleration in the Y direction will be Asinθ.

 

[jbriggs444]

Do I have to choose the same coordinate system for the wedge that I chose for block? If I do so, the component of acceleration in the Y direction will be Asinθ.

You were trying to figure out the normal force. For normal force, what matters is the acceleration of the block in the direction perpendicular to the surface.

You persist in not clarifying whether the acceleration of the wedge is a given fixed constant or whether it is something to be computed. I will assume that it is a given fixed constant, A₀. In that case, the acceleration of the block and of the wedge in the y direction is -A₀sin θ.

Edit: fixed the sign. This is a "downward" acceleration.

With that information in hand, can you now expand ∑F_y = ma_y with all relevant forces?

 

[NoahCygnus]

You were trying to figure out the normal force. For normal force, what matters is the acceleration of the block in the direction perpendicular to the surface.

You persist in not clarifying whether the acceleration of the wedge is a given fixed constant or whether it is something to be computed. I will assume that it is a given fixed constant, A₀. In that case, the acceleration of the block and of the wedge in the y direction is -A₀sin θ.

Edit: fixed the sign. This is a "downward" acceleration.

With that information in hand, can you now expand ∑F_y = ma_y with all relevant forces?

The acceleration on the wedge which you denoted by A, is a constant, and it is towards right.

You were trying to figure out the normal force. For normal force, what matters is the acceleration of the block in the direction perpendicular to the surface.

You persist in not clarifying whether the acceleration of the wedge is a given fixed constant or whether it is something to be computed. I will assume that it is a given fixed constant, A₀. In that case, the acceleration of the block and of the wedge in the y direction is -A₀sin θ.

Edit: fixed the sign. This is a "downward" acceleration.

With that information in hand, can you now expand ∑F_y = ma_y with all relevant forces?

With that information in hand, can you now expand ∑F_y = ma_y with all relevant forces?[/QUOTE]
The acceleration on the wedge which you denoted by A, is a constant, and it is towards right.
Applying Newton's second law to the wedge:
∑Fy = N = MAsinθ

 

[jbriggs444]

Applying Newton's second law to the wedge:
∑Fy = N = MAsinθ

You forgot the sign. That term should be -mA₀ sinθ.
You also missed the force of gravity.

Edit: It is good practice to be consistent with your variable names...

Having used lower case "m" for the mass of the block, you should continue to use "m" and not switch to upper case "M". That way we can reserve "M" for the mass of the wedge.

Having used "A₀" for the rightward acceleration of the wedge, you should not shift to an un-subscripted "A".

At one point in this thread, I had used $\vec{A}$ to refer to the acceleration of the wedge as a vector. More properly, I should have used $\vec{A_0}$.

 

[NoahCygnus]

You forgot the sign. That term should be -mA₀ sinθ.
You also missed the force of gravity.

You forgot the sign. That term should be -mA₀ sinθ.
You also missed the force of gravity.

Edit: It is good practice to be consistent with your variable names...

Having used lower case "m" for the mass of the block, you should continue to use "m" and not switch to upper case "M". That way we can reserve "M" for the mass of the wedge.

Having used "A₀" for the rightward acceleration of the wedge, you should not shift to an un-subscripted "A".

At one point in this thread, I had used $\vec{A}$ to refer to the acceleration of the wedge as a vector. More properly, I should have used $\vec{A_0}$.

Then there is also normal force from the ground on the wedge, let it be N'. I hope you can see the figure, and thank you for trying to help me. I really appreciate it.
All right, let's use A0 for the acceleration of the wedge. Let's apply Newton's second law to wedge;
∑Fy = N'cosθ - Mgcosθ - N = -MA0sinθ

 

[jbriggs444]

Applying Newton's second law to the wedge

Whoah. I missed this. You are applying Newton's 2nd to the wedge?! Try applying it to the block.

 

[NoahCygnus]

Whoah. I missed this. You are applying Newton's 2nd to the wedge?! Try applying it to the block.

Yes, I am applying it to the wedge .
I applied it to the block, and you said that normal force does not remain the same. I asked you why does it change , you said apply Newton's law to the wedge. and choose the same coordinate system that you for the block. I don't know where this is going. Okay let me apply Newton's second law to the block again:
∑Fy = N - mgcosθ = 0 (You said this equation is wrong, normal force is not constant)
∑Fx = mgsinθ = ma (You said this equation is correct)

 

[jbriggs444]

Yes, I am applying it to the wedge .
I applied it to the block, and you said that normal force does not remain the same. I asked you why does it change , you said apply Newton's law to the wedge.

You applied it to the block incorrectly.
I told you to:

Write down a force balance for the block in the y direction. ∑F_y = ma_y

Okay let me apply Newton's second law to the block again:
∑Fy = N - mgcosθ = 0 (You said this equation is wrong, normal force is not constant)

You said that normal force "stayed the same". You did not say what it would be the same as.
I said that no, it did not "stay the same", assuming you had meant that it would stay the same as mg cos θ. So let me clarify. No, it is not given by mg cos θ. Yes, it will be constant.

∑Fx = mgsinθ = ma (You said this equation is correct)

Now then, you wrote down the equation for y:

∑F_y = N - mgcosθ = 0

Where did the ma go? It is not zero.

 

[NoahCygnus]

You applied it to the block incorrectly.
I told you to:
You said that normal force "stayed the same". You did not say what it would be the same as.
I said that no, it did not "stay the same", assuming you had meant that it would stay the same as mg cos θ. So let me clarify. No, it is not given by mg cos θ. Yes, it will be constant.Now then, you wrote down the equation for y:

∑F_y = N - mgcosθ = 0

Where did the ma go? It is not zero.

So, there is also an acceleration in the y direction for the block? I did not know that, I thought the block was only accelerating in x direction. Why is the block accelerating in the y direction?

 

[jbriggs444]

So, there is also an acceleration in the y direction for the block? I did not know that, I thought the block was only accelerating in x direction. Why is the block accelerating in the y direction?

Because it is in contact with the wedge and the wedge is accelerating in the y direction.

If you are going to pick a coordinate system, pick a coordinate system. Do not change willy nilly in mid-problem.

 

[NoahCygnus]

Because it is in contact with the wedge and the wedge is accelerating in the y direction.

If you are going to pick a coordinate system, pick a coordinate system. Do not change willy nilly in mid-problem.

I guess that is the problem. I've been choosing different coordinate system for both the wedge and the block. I thought I had choice to choose different coordinate systems for two different objects.

 

[jbriggs444]

I guess that is the problem. I've been choosing different coordinate system for both the wedge and the block. I thought I had choice to choose different coordinate systems for two different objects.

If you are going to compute a_x and a_y for the block, you should make sure that the x and y directions you use are at right angles. Having chosen a direction for the "x" acceleration of the block, you have no choice for its "y" direction.

If you like, you can use a different coordinate system for the wedge. But then you have to be very careful that you do not blindly assert that A_y for the wedge is zero, therefore a_y for the block must also be zero. Those two y's would be different.

 

[NoahCygnus]

If you are going to compute a_x and a_y for the block, you should make sure that the x and y directions you use are at right angles. Having chosen a direction for the "x" acceleration of the block, you have no choice for its "y" direction.

Of course, I know that. I chose a coordinate system for the block, that had x-axis along the incline, and y-axis perpendicular to it. I chose a coordinate system for the wedge, which I determined forces on the wedge differently, that coordinate system had its x-axis along with ground and y-axis perpendicular to it,

 

[jbriggs444]

Of course, I know that. I chose a coordinate system for the block, that had x-axis along the incline, and y-axis perpendicular to it. I chose a coordinate system for the wedge, which I determined forces on the wedge differently, that coordinate system had its x-axis along with ground and y-axis perpendicular to it,

Fair enough. So can you now compute a_y for the block using the block's coordinate system?

 

[NoahCygnus]

Fair enough. So can you now compute a_y for the block using the block's coordinate system?

I will try, but before that, can you tell me if the block and the wedge momentarily lose contact, as the wedge moves toward right, and then the mgcosθ makes the block accelerate in -y direction? Is that what happens? I can't visualise what happens.

 

[vanhees71]

I thought the wedge is forced to move with constant acceleration in $x$ direction. For me to analyze it using forces is pretty cumbersome, but with the Lagrange method it's pretty simple.

You can also argue easily with the equivalence principle and calculate the effective "gravitational field" in the rest frame of the wedge and then project the force on the block. You'll get something like $F_{\parallel}=-m (g\sin \alpha + a_0 \cos \alpha)$ where $\alpha$ is the direction of the wedge wrt. the $x$ axis.

 

[jbriggs444]

I will try, but before that, can you tell me if the block and the wedge momentarily lose contact, as the wedge moves towards, and then the mgcosθ makes the block accelerate in -y direction? Is that what happens? I can't visualise what happens.

I am going to try to explain it in a way that appeals to my intuition. Perhaps it will appeal to yours.

Suppose the wedge is accelerated to the right with a huge force. Yes, in that case, the wedge will be pulled out from under the block and the block will simply free-fall to the ground. This scenario is too simple to be interesting. So let's not pull the wedge that hard...

Suppose that the system is already in equilibrium at the start of the exercise with just enough normal force so that the block slides down the wedge at a steady acceleration. In this case there is no sudden jerk or loss of contact when we decide to start looking. This is the assumption that I (and I think @vanhees71) would make. We would consider continuing contact between wedge and block to be a "constraint" on the system.

But you seem to have in mind a starting point where the wedge is held motionless, the block is held motionless and we suddenly stop holding things and apply a fixed acceleration to the wedge. In this situation, the system may not start at equilibrium (*). The block may or may not be pressing as tightly into the wedge as it needs to in order to maintain the correct normal force. You could come up with a microscopic description of how this works. If the normal force is too low, the block moves closer to the wedge and is compressed. With compression, the normal force increases. But inertia carries the block past the equilibrium point and and you have too much normal force. You end up with a microscopic oscillation as the block alternately squeezes closer to the wedge and then rebounds. This oscillation would inevitably damp out. But that level of analysis is way too much work and requires detailed information we do not possess. Take it as a given that (unless the wedge gets pulled out too fast) a stable equilibrium will be attained. Observation shows that it will indeed be attained -- and very quickly.

(*) If we are holding all pieces of a system in place, the forces within the system may be "statically indeterminate". That is, there is no way to tell from the idealized description of the setup what all the forces are. For instance, we might be holding the wedge and block tightly against one another or lightly.

 

[vanhees71]

Yes sure, I made the assumption that the block is always gliding along the block. If it gets detached from the block, it's way more complicated of course!

 

[NoahCygnus]

I thought the wedge is forced to move with constant acceleration in $x$ direction. For me to analyze it using forces is pretty cumbersome, but with the Lagrange method it's pretty simple.

You can also argue easily with the equivalence principle and calculate the effective "gravitational field" in the rest frame of the wedge and then project the force on the block. You'll get something like $F_{\parallel}=-m (g\sin \alpha + a_0 \cos \alpha)$ where $\alpha$ is the direction of the wedge wrt. the $x$ axis.

Isn't ma0cosα a fictitious force? As you're introducing a fictitious force , doesn't that mean the result you'll get from the accelerating frame of wedge will be different than the actual result calculated from an inertial frame?

 

[jbriggs444]

Isn't $ma_0 \cos \alpha$ a fictitious force? As you're introducing a fictitious force , doesn't that mean the result you'll get from the accelerating frame of wedge will be different than the actual result calculated from an inertial frame?

Sure, it's a fictitious force. But Newton's second law still applies. The real physical forces that you can calculate using the accelerating frame are the same as the real physical forces that you would calculate using an inertial frame.

The accelerations that you calculate in the accelerating frame would indeed need to be adjusted (aka "transformed") before they are correct for the ground frame. But adopting the accelerating frame may simplify the analysis enough that it's worth the added effort of a transformation step at the end.

 

[NoahCygnus]

Sure, it's a fictitious force. But Newton's second law still applies. The real physical forces that you can calculate using the accelerating frame are the same as the real physical forces that you would calculate using an inertial frame.

The accelerations that you calculate in the accelerating frame would indeed need to be adjusted (aka "transformed") before they are correct for the ground frame. But adopting the accelerating frame may simplify the analysis enough that it's worth the added effort of a transformation step at the end.

Yes so in the end I'll need to make adjustments to the result obtained from an accelerating frame. I will have to subtract ma0cosα in the end from the result , right ?

 

[zwierz]

Spoiler

perhaps this explanation of what fictitious forces are, would be of some use
https://www.physicsforums.com/threads/normal-force-in-a-curvilnear-motion.913890/#post-5758016

 

[jbriggs444]

Yes so in the end I'll need to make adjustments to the result obtained from an accelerating frame. I will have to subtract ma0cosα in the end from the result , right ?

What result did you start with in the accelerating frame? What end result did you wish to obtain?