- #1
NoahCygnus
- 96
- 2
I don't understand the motion of an accelerating wedge and a block. I'd really appreciate if you make me understand the motion in both an inertial and a non inertial reference frame.
Here's a figure I have made, a0 is the acceleration on the wedge with respect to an inertial frame, towards right.
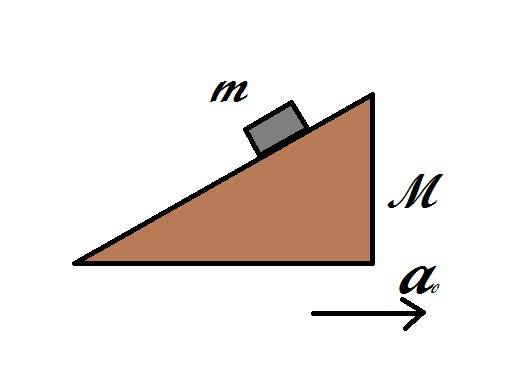
Here's a figure I have made, a0 is the acceleration on the wedge with respect to an inertial frame, towards right.
Last edited: