darwin59
- 12
- 0
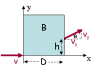
A proton (q = 1.6 X 10-19 C, m = 1.67 X 10-27 kg) moving with constant velocity enters a region containing a constant magnetic field that is directed along the z-axis at (x.,y) = (0,0) as shown. The magnetic field extends for a distance D = 0.7 m in the x-direction. The proton leaves the field having a velocity vector (vx, vy) = (2.2 X 105 m/s, 1.4 X 105 m/s).
http://www.smartphysics.com/images/content/EM/12/h12_bendtheta.png
I have the velocity, but I can't figure out the radius without the magnetic field. Help?
http://www.smartphysics.com/images/content/EM/12/h12_bendtheta.png
I have the velocity, but I can't figure out the radius without the magnetic field. Help?
Last edited by a moderator: