emelie_earl
- 3
- 0
I want to do multiple linear regression, but one of the requirements is the residuals to be normally distributed, and I can check that with QQplots but then the QQ plot shows it is about 95% of data fit into the normal line, but 5% is way off!
can I still proceed ?*or do I have to find a way to transform the data ?*
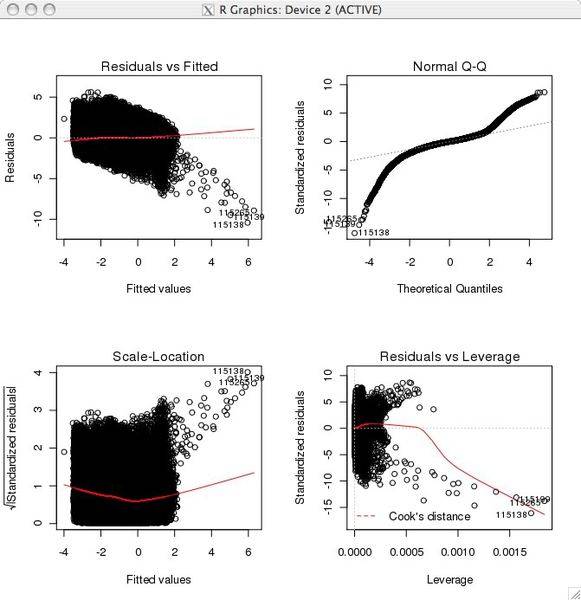
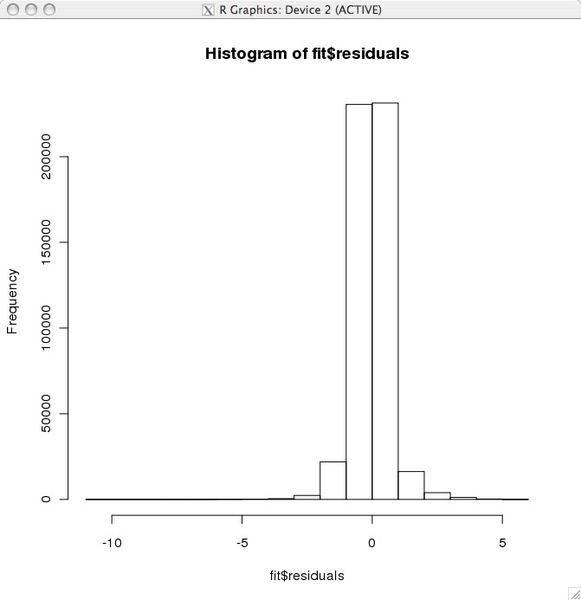
can I still proceed ?*or do I have to find a way to transform the data ?*