- #1
Feodalherren
- 605
- 6
Homework Statement
Homework Equations
The Attempt at a Solution
Umm can somebody explain to me what just happened. None of that makes any sense to me what so ever.
Feodalherren said:Ok I have no idea.. I can't remember what FoG means :/. You didn't even define F as anything?
Feodalherren said:Homework Statement
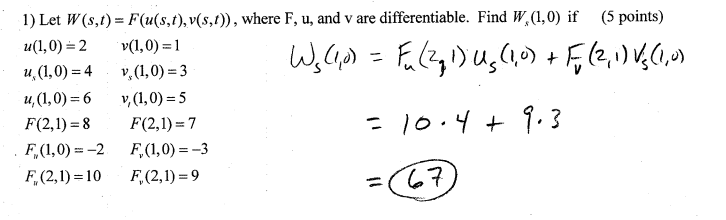
Homework Equations
The Attempt at a Solution
Umm can somebody explain to me what just happened. None of that makes any sense to me what so ever.
Multivariable calculus is a branch of mathematics that deals with the study of functions of multiple variables. It involves the use of derivatives, integrals, and vector calculus to understand and analyze how multiple variables affect a function.
Partial derivatives are a type of derivative that calculates the rate of change of a function with respect to one of its variables, while holding the other variables constant. It helps in understanding how a small change in one variable affects the overall function.
Partial derivatives are used in multivariable calculus to find the critical points of a function, which are points where the partial derivatives are equal to zero. This helps in determining the maximum and minimum values of a function, as well as the direction in which the function is increasing or decreasing.
The main difference between partial derivatives and ordinary derivatives is that partial derivatives deal with functions of multiple variables, while ordinary derivatives deal with functions of a single variable. Partial derivatives also involve holding other variables constant, while ordinary derivatives do not.
Multivariable calculus has various real-world applications such as in physics, economics, engineering, and computer science. It is used to model and analyze complex systems involving multiple variables, such as in optimization problems, motion of objects, and financial models.