Musical frequencies, harmonic or nonharmonic?

[Inquiring_Mind]

Hello! I have this general question regarding (musical) frequencies:

I'm having a bit of a hard time putting what makes logical sense to me, as opposed to what I'm being taught in school. My teacher is basically saying the following: If the fraction/division of two frequencies is rational, the frequencies are harmonic. He goes further by saying: A fraction is rational if the answer completed or periodic. If the fraction results in a non-rational answer, the frequencies are non-harmonic. In an exam question we were asked to match the following frequencies, and write if they are harmonic or non-harmonic:

1) 440 Hz and 780 Hz
2) 380 Hz and 440 Hz
3) 440 Hz and 880 Hz
4) 440 Hz and 670 Hz
5) 230 Hz and 335 Hz

The correct answers in the exam were the following:

1) Harmonic
2) Harmonic
3) Harmonic
4) Non-harmonic
5) Non-harmonic

What I get hung up on is the following. The fraction of all of the frequencies are - in terms of my teacher - periodic or complete. So basically all of them should be harmonic - according to his statement:

1) 440 Hz and 780 Hz

The fraction 440/780 is purely recurring with a period of 6 digits. 440/780 = 22/39 = 0.[564102]

2) 380 Hz and 440 Hz

After an initial decimal the periodicity is 2 decimals. What does an initial decimal apply to a fraction result in this context? 380/440 = 19/22 = 0.863636363636363636363636363636

3) 440 Hz and 880 Hz

This fraction is complete. 440/880 = 1/2 = 0.5

4) 440 Hz and 670 Hz

This fraction 440/670 = 44/67 is purely recurring with a period of 33 digits. 0.[656716417910447761194029850746268]

5) 230 Hz and 335 Hz

This fraction is also purely recurring with a period of 33 digits. 230/335 = 46/67 = 46/67 = 0.[686567164179104477611940298507462]

Now I did check these frequencies in a phase scope and these were my findings:

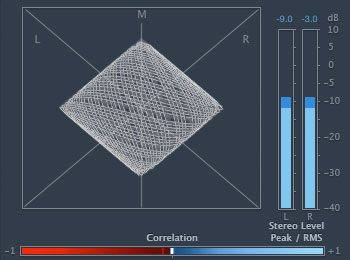
1) 440 Hz and 780 Hz

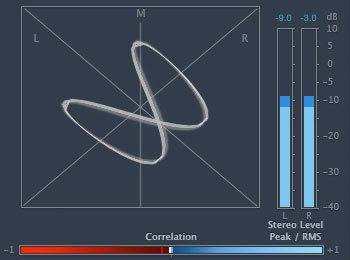
2) 380 Hz and 440 Hz

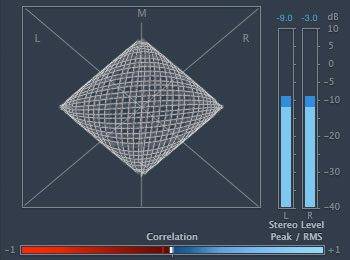
3) 440 Hz and 880 Hz

4) 440 Hz and 670 Hz

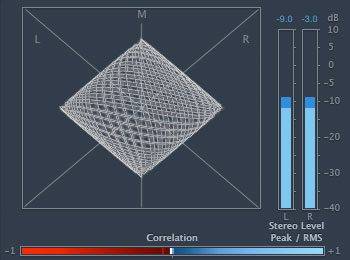
5) 230 Hz and 335 Hz

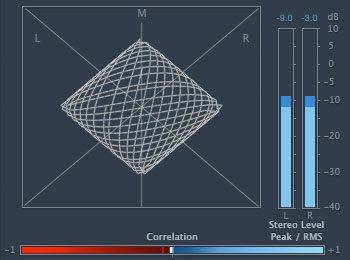
The only frequencies which looks harmonic to me are 440 Hz and 880 Hz. The rest both look and sound non-harmonic to my eyes and ears. Yet, my teacher claims 1 and 2 are harmonic.

Questions:

Q1) Could you please help me understand why for example the interval of 440 Hz and 780 Hz is harmonic? These make up a minor seventh which is 10 cents flat from having just intonation and being consonant according to the overtone series, i.e. 440 Hz and 770 Hz.

Q2) Isn't the definition of harmonic or non-harmonic based on the pythagorean scale and the natural overtone series?

I want the answers in the quiz to be either:

1) Harmonic
2) Harmonic
3) Harmonic
4) Harmonic
5) Harmonic

or

1) Non-harmonic
2) Non-harmonic
3) Harmonic
4) Non-harmonic
5) Non-harmonic

The latter makes most sense to my musical ears and mind. Which is it?

Q3) Is my teacher wrong?

 

[haruspex]

I'm no musicologist, but here are some thoughts...
Your teacher is certainly wrong to suggest that the ratio of two numbers expressed in a finite number of digits could be anything other than rational. If you look at the ratios for the five pairs given:
22 :39
19 :22
1 :2
44 :67
46 :67
what distinguishes the last two from the rest is that they involve numbers > 40. I can imagine one might define consonance by some arbitrary threshold like that, but 40 seems rather high.