sharplens said:
I want equal distance along the arc. That's equivalent to the spoke holes on an oval bicycle rim. Thanks for the nice colorful graph. :)
The method is a bit involved, so please bear with me.
Or jump to the end for the results. ;)Let $a$ be the length of the longest spoke $r_{10}$.
Let $b$ be the length of the shortest spoke $r_{1}$.
First we need to find the arc length of the 90 degree angle, which is:
$$\text{arclength} = \int_0^{\pi/2} s'(t)\,dt = \int_0^{\pi/2} \sqrt{a^2\sin^2 t + b^2\cos^2 t}\,dt$$
Then we need to divide it into 9 equal parts $\Delta s$ for the 10 spokes.
$$\Delta s = \frac 19 \text{arclength}$$
Next is to find the parameters $t_i$ ($i=1,...,10$) where the spokes are.
For that we need to solve:
$$t'(s) = \frac{1}{\sqrt{a^2\sin^2 t + b^2\cos^2 t}}$$
and find the values for $t$ where $s = (i-1)\Delta s$.
And finally we can calculate the lengths of the spokes $r_i$:
$$\text{length }r_i = \sqrt{a^2\cos^2 t_i + b^2\sin^2 t_i}$$I'm afraid we can only evaluate these formulas numerically.
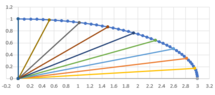
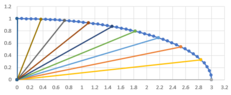
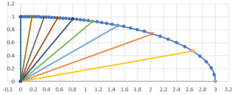
If I do that for $a=r_{10}=3$ and $b=r_{1}=1$, I find an arc length of $3.3412$.
And the spoke lengths are:
$$r_i = 3.0000,\ 2.8572,\ 2.5909,\ 2.2981,\ 2.0020,\ 1.7146,\ 1.4479,\ 1.2202,\ 1.0595,\ 1.0000$$