Need help find fourier transform for revision

[jac7]

I need to find the Fourier transform to this function

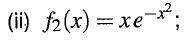and I'm really stuck, because i tried substituting it into the Fourier transform equations but i started to get a really long integral that got out of hand!
i also know that

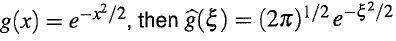but i don't know how to incorporate it into finding the Fourier transform!

If someone could help me get started or give me some tips on easy steps for find the Fourier transform in general it would be much appreciated as my lecturer is away for easter!

Thanks!

 

[HallsofIvy]

The Fourier transform of f(x) is, by definition,
\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty} e^{-ix\zeta}f(x)dx

Your f(x) is xe^{-x^2} so you want to find
\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty} e^{-ix\zeta}xe^{-x^2}dx

If you know how to do it with a "1/2" in the exponent, let y= x\sqrt{2}. Then -y^2= -2x^2 so -x^2= -y^2/2. Of course, dx= dy/\sqrt{2}, so that xe^{-x^2}dx= x(e^{-y^2/2})(dy/\sqrt{2}= (x/\sqrt{2}e^{-y^2}dy= ye^{-y^2}dy.

Now that leaves
e^{-ix\zeta}= e^{-i(y/\sqrt{2})\zeta}= e^{-i(y)(\zeta/\sqrt{2})}

In other words, replace \zeta with \zeta/\sqrt{2} in the Fourier transform.

 

[jac7]

If you know how to do it with a "1/2" in the exponent, let y= x\sqrt{2}. Then -y^2= -2x^2 so -x^2= -y^2/2. Of course, dx= dy/\sqrt{2}, so that xe^{-x^2}dx= x(e^{-y^2/2})(dy/\sqrt{2}= (x/\sqrt{2}e^{-y^2}dy= ye^{-y^2}dy.

I don't understand what you've done here, when i subbed it in like you did i got
(y/2)\sqrt{2pi}e^{-y^2/2}dy

 

[hunt_mat]

Note that if f(x)=\exp (-x^{2}) then

<br /> f(\xi )=\int_{\infty}^{\infty}e^{-x^{2}}e^{ix\xi}dx\Rightarrow f&#039;(\xi )=-2\int_{\infty}^{\infty}xe^{-x^{2}}e^{ix\xi}dx<br />

Does this help?

 

[jac7]

I'm sorry but i can't see where to go next or how it could help!
i know how you got that and i can see how its the same as my function, but you've already got it into transform form? but i need the transform of xf(x), i know that the transform of xf(x) is if'(xi) is it anything to do with that?

 

[eczeno]

hello,

if you know the Fourier transform of e^{-x^2}, then do integration by parts and you will get the solution right away.

i used

dv = x e^{-x^2} dx

cheers

 

[jac7]

integration by part of the transform of exp(-x^2) or integration by parts of exp(-x^2)?

 

[eczeno]

oh, i meant integration by parts on the whole transform:

\int{e^{-ikx} x e^{-x^2}}dx

 

[jac7]

iv tried this and I've ended up with

\frac{-i\xi}{2}\int{e^{-x^2}e^{-ix\xi}}dx

is this right? what do i do next?

 

[eczeno]

good!

the integral is just the Fourier transform of e^{-x^2}, which is given in the problem. you are already done!

the only thing is that i don't get a negative sign when i do the calculation, maybe you lost one along the way somewhere. of course, so might of I, but I'm just doing this for fun, so i will let you check.

cheers

 

[hunt_mat]

I'm sorry but i can't see where to go next or how it could help!
i know how you got that and i can see how its the same as my function, but you've already got it into transform form? but i need the transform of xf(x), i know that the transform of xf(x) is if'(xi) is it anything to do with that?

Bang on, with my idea, you have:

<br /> \hat{f}(\xi )=\sqrt{\pi}e^{-\xi^{2}/4}<br />

To find the integral you require just differentiate the above.

 

[jac7]

good!

the integral is just the Fourier transform of e^{-x^2}, which is given in the problem. you are already done!

the only thing is that i don't get a negative sign when i do the calculation, maybe you lost one along the way somewhere. of course, so might of I, but I'm just doing this for fun, so i will let you check.

cheers

thankyou!

but I'm given the Fourier transform of e^{-x^2/2} is there a simple way of manipulating it so that its the transform of e^{-x^2} or would i have to work that out?

 

[jac7]

Bang on, with my idea, you have:

<br /> \hat{f}(\xi )=\sqrt{\pi}e^{-\xi^{2}/4}<br />

To find the integral you require just differentiate the above.

Thank you very much i think I've finally got it!

just a quick question though, when you did the integration for \hat{f}(\xi ) what limits did you integrate between? because when i integrate between infinity and -infinity I am not getting the same thing because the exponentials just disappear? am i missing something really obvoius?

 

[eczeno]

thankyou!

but I'm given the Fourier transform of e^{-x^2/2} is there a simple way of manipulating it so that its the transform of e^{-x^2} or would i have to work that out?

sure, just do the substitution u=\frac{x}{\sqrt{2}}. i think it will just put a factor of \sqrt{2} out front.

 

[jac7]

Thank you so much for your help!

 

[eczeno]

cheers.