Need help solving/graphing some inequalities

[rought]

Alright again I am having trouble with a few problems.

I am unsure on the first two problem's answers and I have no idea how to do the third one..Solve and graph the solution on a number line

0 < |x + 3| < 1

I get: -3 < X < -2 or -3 > X > -4

and it graphs like this (is this right?) [horrible picture sorry]

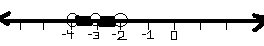
Graph the solution set on a coordinate of axes (I know how to graph it I am just unsure on the points)

1 ≤ |X - 4| ≤ 3

1 ≤ |Y - 4| ≤ 3

I ended up getting

5 ≤ Y ≤ 7 or 3 ≥ Y ≥ 1

and the same for X

5 ≤ X ≤ 7 or 3 ≥ X ≥ 1

Is that right? =/

Ok and this last one I have no idea how to solve

Solve: X^3 + 2x^2 > 3X + 6

 

[rought]

Ok I think I have the first two figured out but I am still stuck on

Solve: X^3 + 2x^2 > 3X + 6

 

[HallsofIvy]

The best way to solve any complicated inequality is to first solve the associated equation.

x³+ 2x²> 3x+ 6 is the same as x³+ 2x²- 3x- 6> 0 and the associated equationj is x³+ 2x²- 3x- 6= 0.

If there are any rational solutions to that they must divide 6 and so are 1, -1, 2, -2, 3, -3, 6, or -6. Trying each of those we see that (-2)³+ 2(-2)²- 3(-2)- 6= -8+ 8+ 6- 6= 0 so x= -2 is a root. Dividing by (x+ 2) we get x²- 3 as quotient and $x= \pm\sqrt{3}$ as the other 2 roots. The numbers, -2, $-\sqrt{3}$, and $\sqrt{3}$ separate all real numbers into four intervals: x< -2, $-2< x< -\sqrt{3}$, $-\sqrt{3}<\sqrt{3}$, and $\sqrt{3}< x$. Since the polynomial x³+ 2x²- 3x- 6 is continuous it can change sign only at those points where it is 0. Check on point in each interval to determine whether the numbers in that interval make the value positive or negative.