rought
- 34
- 0
Alright again I am having trouble with a few problems.
I am unsure on the first two problem's answers and I have no idea how to do the third one..Solve and graph the solution on a number line
0 < |x + 3| < 1
I get: -3 < X < -2 or -3 > X > -4
and it graphs like this (is this right?) [horrible picture sorry]
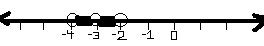
Graph the solution set on a coordinate of axes (I know how to graph it I am just unsure on the points)
1 ≤ |X - 4| ≤ 3
1 ≤ |Y - 4| ≤ 3
I ended up getting
5 ≤ Y ≤ 7 or 3 ≥ Y ≥ 1
and the same for X
5 ≤ X ≤ 7 or 3 ≥ X ≥ 1
Is that right? =/
Ok and this last one I have no idea how to solve
Solve: X^3 + 2x^2 > 3X + 6
I am unsure on the first two problem's answers and I have no idea how to do the third one..Solve and graph the solution on a number line
0 < |x + 3| < 1
I get: -3 < X < -2 or -3 > X > -4
and it graphs like this (is this right?) [horrible picture sorry]
Graph the solution set on a coordinate of axes (I know how to graph it I am just unsure on the points)
1 ≤ |X - 4| ≤ 3
1 ≤ |Y - 4| ≤ 3
I ended up getting
5 ≤ Y ≤ 7 or 3 ≥ Y ≥ 1
and the same for X
5 ≤ X ≤ 7 or 3 ≥ X ≥ 1
Is that right? =/
Ok and this last one I have no idea how to solve
Solve: X^3 + 2x^2 > 3X + 6