Need Help with Vector Problem? Check out Our Easy Solution | Try Now!

[ohheytai]

i uploaded it i can't figure out r subscript n i have no idea can someone help me its my last try thanks

 

[0ddbio]

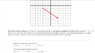
It says that r_{n} and r_{a} give the position with respect to the origin, while r is a relative position vector.

So what vectors would r_{n} and r_{a} be if they start at the origin? Where would the end of those vectors lie? Given that r = r_{n} - r_{a}.
If the answer isn't obvious then review material on graphically subtracting vectors.

 

[ohheytai]

i only have the vector sum though and i don't have those two vectors

 

[cupid.callin]

Note that in a displacement vector r = ra - rb

ra is the vector from origin to head of the vector r
and rb is vector from origin to tail of vector r