New way to find the Circumference of a Circle

MacCormaic · Jan 6, 2015

While I haven't the right technology to find out if the measurement is absolute, it seems that by adding the measurements of A, B, C and D together, you get the circumference of a circle.

(image attached)

Ben Niehoff · Jan 6, 2015

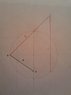
Nope, I'm afraid that gives you

$$2 + \frac{6}{\sqrt{2}} \approx 6.242\ldots$$
assuming a circle of radius 1. This is kind of close to ##2 \pi \approx 6.283\ldots##, but not especially close.

MacCormaic · Jan 6, 2015

Thanks for that Ben. There are several other measurements within the design which brings the measure very close, so it has made me wonder if it is possible to find the circumference of a circle by placing squares inside the circle.

Ben Niehoff · Jan 6, 2015

"Design"? All you did was draw a picture. Since you are doing compass-and-straightedge constructions, every marked length in your diagram is a constructible number. ##\pi## is not even algebraic, let alone constructible, so nothing you can do with a compass and straightedge will ever yield ##\pi##. This was mathematically proven quite some time ago.

jedishrfu · Jan 6, 2015

More on squaring the circle:

http://en.m.wikipedia.org/wiki/Squaring_the_circle

There was two parts to the proof. One was that transcendental numbers can't be constructed and two was tha Pi was a transcendental number.

MacCormaic · Jan 6, 2015

Well Ben I'll be the first to admit I know absolutely nothing about Maths or Geometry or Transcendental numbers. The drawing was merely inspired by reading the book on Infinity by Brian Clegg. While I accept that a circle can't be measured by straight edge and compass, some of the points within the sketch are not whole numbers. I was reading that a computer recently was able to record 13 trillion decimal points in finding the absolute circumference and that there was still a infinity of digits that could be added on. I wasn't trying to prove that a Circle could be squared, I was merely asking if it's possible that the circumference can be derived from another geometrical shaped placed within the circle, where some of the points have decimal measurements. But thanks for working out the equation showing that it was off by a fraction (which is a huge fraction when the circle becomes larger). I do find it difficult to believe that a circumference can't be measured to an absolute number.

phinds · Jan 6, 2015

MacCormaic said: ↑

I wasn't trying to prove that a Circle could be squared, I was merely asking if it's possible that the circumference can be derived from another geometrical shaped placed within the circle...

What this statement says is "I wasn't trying to square the circle, I was just trying to do the same thing as squaring the circle".

MacCormaic · Jan 6, 2015

No, what I asking is, is it possible that there can be a measurement between two points in a geometrical shape (or number of shapes), that when added together with a number of other measurements could make up the equivalent of the circumference of a circle. For example in the attached sketch I would assume that line A from points x + y are never absolute numbers when lines B & C are absolute; so it is possible that the percentage they are off could make them a transcendental number?

phinds · Jan 6, 2015

MacCormaic said: ↑

No, what I asking is, is it possible that there can be a measurement between two points in a geometrical shape (or number of shapes), that when added together with a number of other measurements could make up the equivalent of the circumference of a circle.

Exactly. You are asking if it is possible to do the equivalent of squaring the circle.

jedishrfu · Jan 6, 2015

If I draw a number line, I know PI lies between 3 and 4 but there is no way to construct an intersection that will cross the number line at PI. I can get arbitrarily close but I can never say definitively that the intersection is PI. It has to do with constructible numbers and PI being transcendental can't be constructed.

MacCormaic · Jan 6, 2015

Ok, so the mathematical definition you are saying is that any attempt to find the measurement using lines is termed an attempt to square the circle, which is absolutely impossible. Thanks for the imput.

phinds · Jan 6, 2015

MacCormaic said: ↑

Ok, so the mathematical definition you are saying is that any attempt to find the measurement using lines is termed an attempt to square the circle, which is absolutely impossible. Thanks for the imput.

Exactly.

Think about it this way. If you can use a compass and ruler to construct a set of straight lines which when added up equal the circumference of a circle, you can just to this:

Using the same compass/ruler, transfer the line segments all onto one straight line. Divide that line into 4 equal parts (trivial with compass/ruler). You now have the sides of a square, the perimeter of which is the same as the circumference of the original circle. This is called squaring the circle. It is not possible.

Log in or Sign up

New way to find the Circumference of a Circle

MacCormaic

Attached Files:

IMG_20150106_143512.jpg

Ben Niehoff

MacCormaic

Ben Niehoff

jedishrfu

Staff: Mentor

MacCormaic

phinds

MacCormaic

Attached Files:

IMG_20150106_185237.jpg

phinds

jedishrfu

Staff: Mentor

MacCormaic

phinds

A new way to raise your children? (Replies: 2)

New way of growing coconuts? (Replies: 14)

What's The Best Way To Learn A New Subject? (Replies: 13)

Learning a new language: the best way to go about it? (Replies: 5)

New (old) keyboard is on the way. (Replies: 6)