x2017
- 84
- 1
Homework Statement
Homework Equations
ΣM=Στ
The Attempt at a Solution
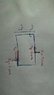
I know how to get the net torque about point P, but I am having difficulty determining where the moment arms for each force should be. I did 9 simpler questions before this no problem, but this diagram is a bit more complicated and I'm having trouble with it. The last three questions I have to do are all exactly the same (this one) with different numbers, so some help would be greatly appreciated!
I know the moment arm is the perpendicular distance from the line of action of the force to the point of rotation.
I am confused as how to find the length of the moment arms in this particular diagram. I think they should look like this (orange and blue lines)
But I am lost as to how to get their lengths (if where I have them is even correct).