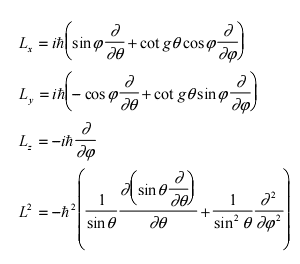I No r dependence in L operator?

[DoobleD]

In classical mechanics, angular momentum, L = r x p, depends of r. For a given momentum p, the bigger r is, the bigger is the angular momentum. Event in spherical coordinates, r still appears in the classical angular momentum.

However, the angular momentum operator in QM has no r dependence, it's only a function of angles phi and theta. While I can follow the derivation of the operator, I find it surprising that the r dependency vanishes. How can we explain this physically ?

 

[BvU]

https://faculty.washington.edu/seattle/physics227/reading/reading-24-25.pdf

 

[DoobleD]

Thank you. Is there a specific part adressing my question ? This seem to be quite complete course on QM angular momentum, but after a quick search all I have found regarding r, is around the end when it says they haven't adressed r yet. But they refer to the case of the hydrogen atom I think, which has a hamiltonian with a r dependent potential.

 

[BvU]

First page

 

[DoobleD]

After reading it I don't see where is it ? It shows how we derive the QM version of angular momentum from the classical picture. This doesn't bother me. And even if the maths of this derivation also works out for the angular momentum operator, I just wonder, on a conceptual level, why the r dependence vanishes.

 

[Nugatory]

After reading it I don't see where is it ?

The $x$, $y$, and $z$ that appear in the first page are the components of $\vec{r}$. So it's there.

 

[DoobleD]

The $x$, $y$, and $z$ that appear in the first page are the components of $\vec{r}$. So it's there.

Right, I should have been more precise : why r vanishes in the spherical coordinate version of L ?

 

[BvU]

Math, math and math. The transition from cartesian to spherical makes it look like a magic disappearance, I concede.

http://quantummechanics.ucsd.edu/ph130a/130_notes/node216.html

My hunch is the dependence sits in the wavefunction itself, but I quit trying to form such mental pictures a long time ago.
I do feel with you, so let's ask @Nugatory whether this is only seemingly counter-intuitive, or whether there's some other insight we overlook ...

 

[DoobleD]

I do feel with you, so let's ask @Nugatory whether this is only seemingly counter-intuitive, or whether there's some other insight we overlook ...

Exactly. Good to know I am not alone. :D I came across the same link BTW searching an answer on Google.

 

[DoobleD]

What adds to the weirdness is that angular momentum in classical mechanics, even if expressed in spherical coordinates, does have a r dependency :

https://courses.washington.edu/bhrchem/c455/classical_mechanics.pdf (page 11).

 

[blue_leaf77]

Since it has been confirmed by many experiments that such formulation of angular momentum operator does work, I think I will just accept it as granted. Besides that, angular momentum is defined as the generator of rotation in space in quantum mechanics, so I think it makes sense that it should not depend on r.

 

[PeterDonis]

In classical mechanics, angular momentum, L = r x p, depends of r. For a given momentum p, the bigger r is, the bigger is the angular momentum. Event in spherical coordinates, r still appears in the classical angular momentum.

However, the angular momentum operator in QM has no r dependence

The quantum operator has no $r$ dependence, but that does not mean the actual measured values of angular momentum have no $r$ dependence. The latter is what you would expect to be analogous to the classical angular momentum.

 

[DoobleD]

The quantum operator has no rrr dependence, but that does not mean the actual measured values of angular momentum have no rrr dependence. The latter is what you would expect to be analogous to the classical angular momentum.

Right ! So, as @BvU suggested, the r dependence would be in the wavefunction ? But...The eigenstates of the angular momentum operator are spherical harmonics, which are not functions of r, but of theta and phi only.

 

[PeterDonis]

The eigenstates of the angular momentum operator are spherical harmonics

No, they are spherical harmonics combined with a function of $r$ only.

 

[DoobleD]

No, they are spherical harmonics combined with a function of

Do you mean if the particle is in a r-dependent potential ? The courses I read present the eigenstates of L as being solely spherical harmonics. After a quick search on Google, same thing.

 

[BvU]

central potential, e.g. hydrogen atom allows separation into radial and angular eigenfunctions. L is 'on the angular side'

 

[DoobleD]

central potential, e.g. hydrogen atom allows separation into radial and angular eigenfunctions. L is 'on the angular side'

Yes I have seen that separation in the case of the hydrogen atom. But I'm trying to consider L just for itself, outside any specific potential considerations. Maybe this doesn't make sense then ?

 

[DoobleD]

Well, I suppose I am considering the case of a free particle then. And it is true that even in classical mechanics, the angular momentum of a free particle is a constant, so not really dependent of r. Mmh, is this a viable answer ? I'm not sure at all. :D

 

[PeterDonis]

I'm trying to consider L just for itself, outside any specific potential considerations. Maybe this doesn't make sense then ?

No, it doesn't. Any quantum system will have some Hamiltonian, and therefore some potential. That determines the energy eigenstates, and it's meaningless to talk about the action of any operator, including L, without some specification of the states it's acting on.

 

[DoobleD]

Any quantum system will have some Hamiltonian, and therefore some potential.

What about the free particle case ?

 

[BvU]

Take a free particle wave function and see what $L$ does ...

 

[Nugatory]

What about the free particle case ?

Then the Hamiltonian is $p^2/2m$, with $V=0$.

 

[vanhees71]

Of course the orbital angular-momentum operators,
$$\hat{\vec{L}}=\hat{\vec{x}} \times \hat{\vec{p}}$$
make sense for themselves. They obey the commutation relation of the Lie algebra so(3) of the rotation group SO(3),
$$[\hat{L}_j,\hat{L}_k]=\mathrm{i} \epsilon_{jkl} \hat{L}_l,$$
where I've used units with $\hbar=1$ to make things simpler.

Now you can show that there's a common eigenbasis for $\hat{\vec{L}}^2$ and $\hat{L}_z$ with eigenvalues $l(l+1)$ and $m \in \{-l,-l+1,\ldots,l-1,l \}$, where $l \in \{0,1,2,\ldots \}$.

In position representation, using spherical coordinates, the eigenfunctions are the spherical harmonics $Y_{lm}(\vartheta,\varphi)$. Since $\hat{\vec{L}}$ commutes with $\hat{r}=|\hat{\vec{x}}|$ you can multiply it with any function of $r$. So any wave function of a single spin-0 particle can be expanded in spherical harmonics
$$\psi(\vec{x})=\sum_{l=0}^{\infty} \sum_{m=-l}^{l} R_{lm}(r) Y_{lm}(\vartheta,\varphi).$$

 

[DoobleD]

Of course the orbital angular-momentum operators,
$$\hat{\vec{L}}=\hat{\vec{x}} \times \hat{\vec{p}}$$
make sense for themselves. They obey the commutation relation of the Lie algebra so(3) of the rotation group SO(3),
$$[\hat{L}_j,\hat{L}_k]=\mathrm{i} \epsilon_{jkl} \hat{L}_l,$$
where I've used units with $\hbar=1$ to make things simpler.

Now you can show that there's a common eigenbasis for $\hat{\vec{L}}^2$ and $\hat{L}_z$ with eigenvalues $l(l+1)$ and $m \in \{-l,-l+1,\ldots,l-1,l \}$, where $l \in \{0,1,2,\ldots \}$.

In position representation, using spherical coordinates, the eigenfunctions are the spherical harmonics $Y_{lm}(\vartheta,\varphi)$. Since $\hat{\vec{L}}$ commutes with $\hat{r}=|\hat{\vec{x}}|$ you can multiply it with any function of $r$. So any wave function of a single spin-0 particle can be expanded in spherical harmonics
$$\psi(\vec{x})=\sum_{l=0}^{\infty} \sum_{m=-l}^{l} R_{lm}(r) Y_{lm}(\vartheta,\varphi).$$

Yes all of that is essentially what a textbook presents. But that doesn't tell why r doesn't appear in L operator. If there is such an answer in the first place of course, maybe there is nothing more here other than "the maths works out that way, and the model matches experiments", I don't know.

In the last equation you wrote, the function of r is "artifically" added in the mix so that we get a generic state for any potential. Or it is added by necessity if we solve the hamiltonian of the hydorgen atom. But it doesn't come from a requirement of the L operator itself. The L operator in itself doesn't care about r, neither do its eigenstates. That just seems weird to me, when compared to classical angular momentum. The classical angular momentum does have a r dependency, without the need for any particular potential or further assumption. It is part of its definition. The QM L operator in itself (and its eigenstates) is only concerned with angles.

EDIT: I should have written L operator in spherical coordinates, every time I wrote L.

Take a free particle wave function and see what LLL does ...

Seems a very reasonable thing to do. :D I'll try that as soon as I can.

 

[vanhees71]

The angular momentum operator is the generator for rotations. The length of the vector is not affected by rotations (which is the definition of rotations in the first place). So it's intuitive that the angular-momentum operator does not depend on $r$. Also the expansion of the wave function in terms of spherical harmonics given in my previous posting is not "artificial" but very natural thinking in terms of generalized Fourier transformations. Here we expand in terms of angular-momentum eigenfunctions. The reason why this is a clever expansion is that the Laplace operator separates in spherical coordinates. This you find indeed in any good textbook on quantum theory.

 

[DoobleD]

The angular momentum operator is the generator for rotations. The length of the vector is not affected by rotations (which is the definition of rotations in the first place). So it's intuitive that the angular-momentum operator does not depend on rrr

Right. But then, why does the classical angular momentum, even expressed in spherical coordinates, depends on r ?

Also the expansion of the wave function in terms of spherical harmonics given in my previous posting is not "artificial" but very natural thinking in terms of generalized Fourier transformations. Here we expand in terms of angular-momentum eigenfunctions.

The expansion in terms of the spherical harmonics is not artificial, that's not what I said. The addition of the function of r in front of the spherical harmonics, is artifcial. Or required in certain problems. It is not required by the angular momentum operator.

 

[blue_leaf77]

But then, why does the classical angular momentum, even expressed in spherical coordinates, depends on r ?

My answer might not satisfy you, but the independency of $\mathbf L$ on $r$ is all a mathematical consequence of how we chose quantum mechanics to work in a way that we understand today. The formula $\mathbf L = \mathbf r \times \mathbf p$ is not the general formula for an angular momentum as formulated in QM, in fact it's a consequence of $\mathbf L\cdot \hat n$ being defined as a generator of rotation around the direction specified by $\hat n$. It's also the point where the formulation for angular momentum in QM and classical mechanics intersects, namely in both realms an angular momentum is a generator of rotation.
Imagine you want to rotate a wavefunction $\psi(x,y,z)$ through an infinitesimal angle $\Delta \theta$ around z-axis in position space (our physical dimension). If your initial wavefunction is
$$\psi(x,y,z)$$
then the rotated wavefunction will be
$$ \psi(x+\Delta \theta y, y-\Delta \theta x,z) $$
You want to find an operator which does this kind of transformation, which is a rotation operator. The expression for an infinitesimal symmetry transformation is given by
$$ 1- ia \hat O $$
where $\hat O$ is the so-called symmetry transformation generator and $a$ the amount of infinitesimal change that $\hat O$ induces on the object it acts on. In short you want to find $\hat O$ such that
$$(1- i\Delta \theta \hat O) \psi(x,y,z) = \psi(x+\Delta \theta y, y-\Delta \theta x,z) $$
Given that $\Delta \theta$ is infinitesimal, the RHS can be rewritten as
$$
\psi(x-\Delta \theta y, y+\Delta \theta x,z) = \psi(x,y,z) + y \Delta \theta \frac{\partial \psi}{\partial x} - x \Delta \theta \frac{\partial \psi}{\partial y} \\
= \left( 1 - \frac{i}{\hbar} \Delta \theta (x p_y - y p_x) \right)\psi(x,y,z)
$$
where the definition $\mathbf p = -i\hbar \nabla$ (which can as well be another of your wonder why the momentum operator does not depend on mass and velocity) has been used. Therefore, the operator that we demanded to induce rotation around z-axis is actually
$$
\hat O = (x p_y - y p_x) = (\mathbf r \times \mathbf p)_z = L_z
$$
Repeating the same procedure above for the other rotation around x and y axis, it should be straight forward to see that they are equal to $L_x$ an d $L_y$ respectively.
The point is that, just because we have used $\mathbf p = -i\hbar \nabla$ (which actually comes from the requirement that momentum should generate a translation space) the angular momentum operator turns out to be independent on $r$ when expressed in spherical coordinate. Earlier in this post I emphasized that the angular momentum we have discussed up to now only generates rotation in position space, this was specified because you can define another generator of rotation in different space, such as the space of spin, wherein the angular momentum is no longer expressible as $\mathbf r \times \mathbf p$. This last expression, again, is not the general formula, it's derivable from a more fundamental concept.

 

[samalkhaiat]

In classical mechanics, angular momentum, L = r x p, depends of r. For a given momentum p, the bigger r is, the bigger is the angular momentum.

In classical mechanics, the linear momentum vector is \vec{p} = m \vec{v}. In QM, the linear momentum operator is \hat{p} = -i\hbar \nabla. Where did the mass m and velocity \vec{v} go? The answer is given by the quantization rule m \frac{d\vec{r}}{dt} \to -i\hbar \frac{d}{d\vec{r}} .

Event in spherical coordinates, r still appears in the classical angular momentum.

You can make r “disappear” even in classical mechanics. In terms of the pairs (\theta , p_{\theta}) and (\phi , p_{\phi}), the classical angular momentum vector \vec{L} = \vec{r} \times \vec{p} has the form
<br /> \vec{L} = \begin{pmatrix}<br /> - \sin \phi \ p_{\theta} - \cot \theta \cos \phi \ p_{\phi} \\<br /> \cos \phi \ p_{\theta} - \cot \theta \sin \phi \ p_{\phi} \\<br /> p_{\phi}<br /> \end{pmatrix} .<br />
From this classical expression for \vec{L} you obtain the quantum operator \hat{L} by applying the above mentioned quantization rule: p_{\theta} = mr^{2}\frac{d \theta}{dt} \to \hat{p}_{\theta} = - i\hbar \frac{\partial}{\partial \theta} ,p_{\phi} = mr^{2} \sin^{2} \theta \frac{d \phi}{dt} \to \hat{p}_{\phi} = - i\hbar \frac{\partial}{\partial \phi} .

 

[DoobleD]

@blue_leaf77, thank you very much, this does answer the question ! The key point here I wasn't really aware of is that the formula L = r x p is a consequence of the fact that angular momentum is the generator of rotation, and not the other way around. This seems quite obvious now, as this new (for me) definition of angular momentum seems much more fundamental, but I never thought about it this way before.

Then things flow naturally. I don't know that much maths about symmetry transformations, but if I trust the expression for an infinitesimal symmetry transformation you give, then it works out nicely. And I don't bother the absence of r in the end anymore because I drop the L = r x p as the fundamental definition of L.

which can as well be another of your wonder why the momentum operator does not depend on mass and velocity

Yes I was wondering this as well. This is now answered too ! :D Same reason, but with generator of translation.

I am also trying to relate this to Noether's theorem. I already knew that conservation of momentum implies translation symmetry, and actually only applies to canonical momentum, which is not always p = mv. But I didn't make the conceptual shift that symmetry transformations are the actual fundamental "definitions" for momentum ((translation symmetry) and angular momentum (rotation symmetry).

This is a big "upgrade" in my humble understanding of physics. Thanks again !

 

[blue_leaf77]

if I trust the expression for an infinitesimal symmetry transformation you give

The symmetry operator for a finite amount of transformation is $e^{-ia\hat O}$. This is obtainable by repeatedly applying the infinitesimal form $1-i\frac{a}{n}\hat O$ $n$ times and let $n$ approaches infinity.
$$
e^{-ia\hat O} = \lim_{n\to \infty} \left(1-i\frac{a}{n}\hat O\right)^n
$$
which can be seen to hold if you take the analogy with the limit definition of $e$.

Thanks again !

You are welcome. Good to know if it helps.

 

[Demystifier]

I find it surprising that the r dependency vanishes. How can we explain this physically ?

A simple heuristic argument is to use the Bohr quantization condition of "old" quantum mechanics
$$L=n\hbar$$
which clearly does not depend on $r$. For a quick "derivation" of this condition see the second box in
http://hyperphysics.phy-astr.gsu.edu/hbase/Bohr.html

 

[Karolus]

I try to answer, let's see ... The mistake I think you try to find an analogy with the case "classic." But unfortunately does not go very far, in the classical case it makes sense to speak of a physical object rolling. In MQ, for example, we associate an angular momentum to the electron, which also has a "radius", but can not conceive an object as "rotating". For example, the photon has a spin equal to 1, but how do you represent a photon "rotating" on itself? In addition, the electron orbital angular momentum would make sense if it were a solid macroscpic object that rotates on itself, and it is not the quantum case. Any analogy with the classical case vanishes, as vanishes r. The same "radius" r is not a concept that has an analogy with the classical case. (Positions and spatial coordinates are "operators"). So the only thing consistent in your hand is the electron wave function, and the only thing you can do is calculate the eigenstates of L applied to $\psi$ . The rest of the work it does mathematics..

 

[Karolus]

we see it in a more concrete way a little bit maybe you can somehow get closer to a "picture" classic. Indeed on "large atoms" for example with more electrons, you would expect a "big angular momentum" as a fact (in a quantum) occurs.
Let us take the simplest case of the hydrogen atom in a first approximation, only Coulomb potential without further correction, relativistic spin-orbit etc.
The eigenfunctions of the Hamiltonian are of the type: $\psi_ {nlm} (\ r, \Theta, \Phi) = \ R_ {nl} (\ r) \ Y ^ {m} _ {l} (\Theta, \Phi)$
These are eigenfunctions of the total angular momentum $\hat {\mathbf L}^2$ eigenvalues $\hbar ^2l (l + 1)$
Where n, l and m are respectively the main quantum numbers, angular momentum and angular orientation with respect to an axis.
The condition on the number l is : $0 \leq l \leq n-1$
So, effectively increasing the quantum number n, the quantum number can take on progressively higher values with "more" angular momentum as a mechanic.
Remember that the shape of the wave function is spherical only in the case n = 1, but with n higher this shape is complicated, assuming shapes or ellipsoids with lobes arranged on the axes, for which it is impossible to speak of a "radius", although in the spherical case we can speak of "radius" only in a probabilistic sense