Proofs in analytic geometry and vector spaces.

[LCSphysicist]

Homework Statement

All below

Relevant Equations

N/A

I was just thinking, if is said to me demonstrate any geometry statement, can i open the vector in its vector's coordinates? I will say more about:

For example, if is said to me: Proof the square's diagonals are orthogonal, how plausible is a proof like?:

d1 = Diagonal one = (a,b,c)
d2 = Diagonal two =(-a,-b,c)

but a² + b² = l² = c²

d1*d2 = (-a² -b² + c²) = (-(a² + b²) + c²) = > This is the dot product

The problems i see is:

#1 = I adopt a R3 space.
#2 = I assumed the basis orthogonal, so the distance between the vertex lying in the same side is (a²+b²)^(1/2)

The dot product holds for any basis anyway.

Can someone say: "(This is not a general proof, you adopt the orthogonal basis and R3)"?

We could try to proof by plane geometry, this is the general proof?

OBS: There is too

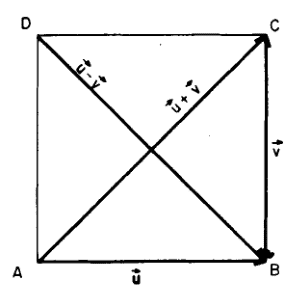
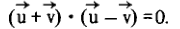(the rest is easy)

What seems to me more general proof.

 

[Delta2]

There is indeed a problem with #2, you have to prove that it holds in any base but i don't understand the problem with #1, how are you supposed to work with vectors if you don't adapt a vector space(R^3 or R^2)?

You are right that the proof with u and v is more general more complete i would say.