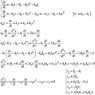Nonlinear coupled differential equation system - kinetics

[LiAlH4]

Dear All,

Recently, I have measured a series of nonlinear vibrational spectra from which I would like to extract some useful information about kinetics of the exchange process occurring in the studied system.
I need to fit my experimental data to kinetic model that is a solution of coupled differential equations of this form:
<br /> \frac{\mathrm{d}x(t) }{\mathrm{d} t} = -k_1x(t)-k_2-k_3x^2(t)+k_4y(t) \\ \\<br /> \frac{\mathrm{d}y(t) }{\mathrm{d} t} = -k_5y(t)-k_6+k_3x^2(t)-k_4y(t)<br />
where k_1,k_2,k_3,k_4,k_5,k_6 are constants

Do you think that this system has got an analytic solution? What kind of method should I use to find it?
I have tried assuming the solution to be series of hyperbolic functions but I failed to determine the expansion coefficients.

Thank you in advance and have a nice day,

Michael

 

[JJacquelin]

Hi !
The system can be reduced to a second order non linear equation, which is too complicated to be solved analytically, on my opinion.

 

[LiAlH4]

Thank you very much for your reply. I will try to make use of numerical solution then.