- #1
- 4,807
- 32
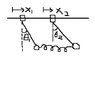
I have a book here that says that the number of normal modes is equal to the number of degree of freedom of a system. I'm wondering if this applies to just about any system or only to systems in which every coordinates can oscillate harmonically. The question is not very well formulated, so I included a picture. (The support of the pendulums can slide along the horizontal line)
This system has 4 degrees of freedom. Does it have 2 or 4 normal modes of oscillations?
This system has 4 degrees of freedom. Does it have 2 or 4 normal modes of oscillations?
Attachments
Last edited: