badvot
- 5
- 1
- Homework Statement
- Calculate the macroscopic cross section using volume fractions
- Relevant Equations
- Macroscopic nuclear cross section
This question is in the book " Introduction to nuclear engineering by Lamarsh" Chapter3:

I think it's pretty basic but I couldn't find the proper way to prove it, and now I even suspect that it's not a correct question.
My attempt solution:
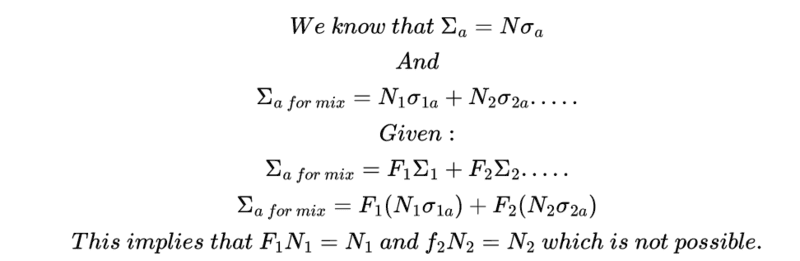
I would very much appreciate your help. Thanks in advance.
I think it's pretty basic but I couldn't find the proper way to prove it, and now I even suspect that it's not a correct question.
My attempt solution:
I would very much appreciate your help. Thanks in advance.
