- #1
- 1,782
- 32
Hi,
I wrote a piece of MATLAB code to compute a double integral of the form:
[tex]
\int_{a}^{b}\int_{c}^{d}f(x,y)dxdy
[/tex]
I went about it using the trapezium rule, so what I did was apply the rule to the [itex]x[/itex] variable first to obtain:
[tex]
\int_{a}^{b}\int_{c}^{d}f(x,y)dxdy\approx\frac{\delta x}{2}\int_{c}^{d}2\sum_{i=1}^{N}f(x_{i},y)-f(a,y)-f(b,y)dy
[/tex]
I then went on to apply the trapezium rule in the [itex]y[/itex] variable to obtain:
[tex]
\begin{array}{rcl}
\int_{a}^{b}\int_{c}^{d}f(x,y)dxdy & = & \left(\sum_{i=1}^{N}\sum_{j=1}^{M}f(x_{i},y_{j})-\frac{1}{2}\sum_{i=1}^{N}f(x_{i},c)-\frac{1}{2}\sum_{i=1}^{N}f(x_{i},d)\right)\delta x\delta y \\
& - & \frac{1}{2}\left(\sum_{j=1}^{M}f(a,y_{j})-\sum_{j=1}^{M}f(b,y_{j})\right)\delta x\delta y \\
& - & \frac{1}{2}(f(a,c)+f(b,c)+f(a,d)+f(b,d))\delta x\delta y
\end{array}
[/tex]
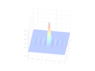
I tried using this to compute the inverse Fourier transform of the 2d Gaussian and I got some rather bad results.
I include the results. Not what I expected.
I wrote a piece of MATLAB code to compute a double integral of the form:
[tex]
\int_{a}^{b}\int_{c}^{d}f(x,y)dxdy
[/tex]
I went about it using the trapezium rule, so what I did was apply the rule to the [itex]x[/itex] variable first to obtain:
[tex]
\int_{a}^{b}\int_{c}^{d}f(x,y)dxdy\approx\frac{\delta x}{2}\int_{c}^{d}2\sum_{i=1}^{N}f(x_{i},y)-f(a,y)-f(b,y)dy
[/tex]
I then went on to apply the trapezium rule in the [itex]y[/itex] variable to obtain:
[tex]
\begin{array}{rcl}
\int_{a}^{b}\int_{c}^{d}f(x,y)dxdy & = & \left(\sum_{i=1}^{N}\sum_{j=1}^{M}f(x_{i},y_{j})-\frac{1}{2}\sum_{i=1}^{N}f(x_{i},c)-\frac{1}{2}\sum_{i=1}^{N}f(x_{i},d)\right)\delta x\delta y \\
& - & \frac{1}{2}\left(\sum_{j=1}^{M}f(a,y_{j})-\sum_{j=1}^{M}f(b,y_{j})\right)\delta x\delta y \\
& - & \frac{1}{2}(f(a,c)+f(b,c)+f(a,d)+f(b,d))\delta x\delta y
\end{array}
[/tex]
I tried using this to compute the inverse Fourier transform of the 2d Gaussian and I got some rather bad results.
I include the results. Not what I expected.
Last edited:
 ;
;