DanielA
- 27
- 2
- TL;DR
- I am following a paper which solves the system with an eigenvalue solver alone using an initial guess and SCF calculations https://www.mdpi.com/2218-2004/6/2/22?type=check_update&version=2#related_content
Here is the paper again: https://www.mdpi.com/2218-2004/6/2/22?type=check_update&version=2#related_content
For a class project I need to calculate the energy levels of atoms using the Hartree Fock method as presented in this paper which essentially brute forces the calculation using finite difference matrices to write the Hartree-Fock equations as a matrix equation solved by standard eigenvalue solvers instead of using other more subtle approaches.
However, I am failing to achieve convergence whatsoever and my energies are oscillating. Considering my inexperience with problems like this, I'm worried that I'm misunderstanding the work at a basic numerical level. I also probably don't understand how the results are being presented and what is going into converting between numerical results and the final plots/energies since Hartree-Fock energies aren't the real energy of the electrons like a true Schrödinger equation. The paper compares the difference in energy results to https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable5.htm which makes sense since we don't calculate the ground state energy to get a zero point. I assume the 1s2s level is the sum of the two electron energies the rescaled by adding the 1s^2 state.In the broad stroke, the process is simple. Hartree Fock theory separates a multi electron wave function into N individual single electron eigenvalue equations which must be solved iteratively because the operator depends on the other wave functions.
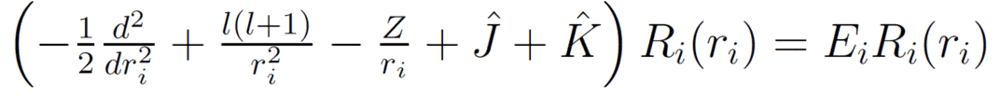
The first term can be written as a tridiagonal matrix using finite-difference coefficients as found in the paper. The second and third terms are as written diagonal matrices.
The 4th, Hartree, term the spherically averaged coulomb repulsion an electron feels from all the other electrons. It is also diagonal and represents the average coulomb force experienced by the ith electron by all others. It, and the exchange term require knowledge of the position radial wave functions of the other electrons. I am familiar with the algebra to derive the expression as written.
The exchange term, K, is a dense matrix also dependent on the other wave functions, but also on the spin and angular momentum relations between the electrons. The V_k term is found in the paper and is related to the wigner 3-j terms. The last student to do this problem couldn't achieve convergence with this matrix and had to make an approximation. Tonight I'll implement that change and see if it's the real issue, but I don't see why this expression won't work.
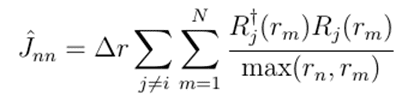
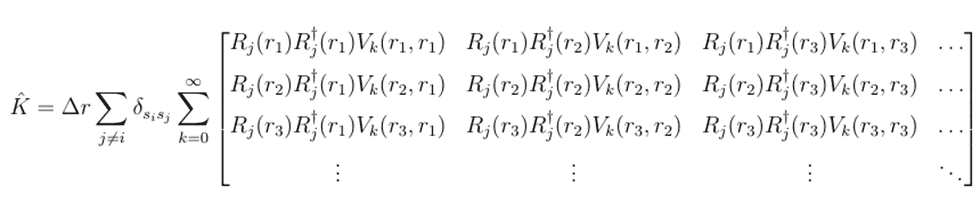
The process is as follows for helium:
1. Initialize the wave functions as the energy level dependent solution of the hydrogen atom hamiltonian with Z = 2, which I solved for numerically and have an accurate solution for in terms of atomic units out to arbitrary radius (ie bohrs and hartrees). ie if I want to study the 1s2s configuration I would set the first electron to the 1st eigenfunction and the second electron to the second eigenfunction.
Problem: This is probably a dumb question, but as far as I can tell, although the energies are right, the total solution doesn't seem close to normalized. I numerically integrated the radial portion as $$\int{r^2*\Psi^{*}*\Psi}dr$$ and got 0.1501 which, since the spherical portion of the hydrogen atom is 1 by design, means this doesn't seem to be normalized.
The paper, and other resources don't talk about it, but when doing numerical calculations do I need to worry about normalization of a wave function? I'd assume no, because in the end it's just a scaling number and should be calculable at the end of everything. Additionally, I tried to normalize my functions at different points in the code, and it actually caused convergence... at an energy of about 50 hartree for both electrons.
2. I initialize my electrons, and calculate my operator for both electrons individually using the above equation which is easy to implement in matlab. I can upload my code later, but I've checked it too many times at this point for the implementation to be the issue assuming the equations are right.
3. I use eigs function in MATLAB to solve for the lowest energy eigenvalues and eigenfunctions of the system to save time. For the ground state I'd only need to calculate the first one and for first excited I can calculate the first two (and use the second).
4. I compare the energy change of each electron individually and sum the total change to check for convergence using a 2-norm for the norm function. It's probably better to sum the energy of both electrons and compare it to the sum of the last energy instead, but looking at outputs, that wouldn't suddenly cause my code to converge and if it did, my energy values aren't matching what the paper got for helium.
4a. If I reach convergence I output the exact wave functions I found.
5. If convergence is not reached, I loop again with the electrons set to the new, calculated eigenfunctions where the 1s electron is set to the lowest energy solution of its operator and the 2s electron is set to the second lowest energy of its operator.
I can give more detail if needed, but it's easiest to skim through the paper.
The stepsize is 0.05 bohr out to 30 bohr radius which is low enough to generate a smooth function and avoid issues with missing oscillations of the wave. The wave also clearly converges for helium after ~10 bohr. Calculation speed isn't an issue either as that's essentially the reason the authors took this approach. The code as written in the paper, and in my code is also designed to easily scale to N electrons for higher Z nuclei. I just want to match the helium solution well enough.
I appreciate any help or discussion I can get. At this point I'm just trying to read what I can and try to better understand the numerical methods since I'm essentially just changing random things in my code hoping it works out.
For a class project I need to calculate the energy levels of atoms using the Hartree Fock method as presented in this paper which essentially brute forces the calculation using finite difference matrices to write the Hartree-Fock equations as a matrix equation solved by standard eigenvalue solvers instead of using other more subtle approaches.
However, I am failing to achieve convergence whatsoever and my energies are oscillating. Considering my inexperience with problems like this, I'm worried that I'm misunderstanding the work at a basic numerical level. I also probably don't understand how the results are being presented and what is going into converting between numerical results and the final plots/energies since Hartree-Fock energies aren't the real energy of the electrons like a true Schrödinger equation. The paper compares the difference in energy results to https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable5.htm which makes sense since we don't calculate the ground state energy to get a zero point. I assume the 1s2s level is the sum of the two electron energies the rescaled by adding the 1s^2 state.In the broad stroke, the process is simple. Hartree Fock theory separates a multi electron wave function into N individual single electron eigenvalue equations which must be solved iteratively because the operator depends on the other wave functions.
The first term can be written as a tridiagonal matrix using finite-difference coefficients as found in the paper. The second and third terms are as written diagonal matrices.
The 4th, Hartree, term the spherically averaged coulomb repulsion an electron feels from all the other electrons. It is also diagonal and represents the average coulomb force experienced by the ith electron by all others. It, and the exchange term require knowledge of the position radial wave functions of the other electrons. I am familiar with the algebra to derive the expression as written.
The exchange term, K, is a dense matrix also dependent on the other wave functions, but also on the spin and angular momentum relations between the electrons. The V_k term is found in the paper and is related to the wigner 3-j terms. The last student to do this problem couldn't achieve convergence with this matrix and had to make an approximation. Tonight I'll implement that change and see if it's the real issue, but I don't see why this expression won't work.
The process is as follows for helium:
1. Initialize the wave functions as the energy level dependent solution of the hydrogen atom hamiltonian with Z = 2, which I solved for numerically and have an accurate solution for in terms of atomic units out to arbitrary radius (ie bohrs and hartrees). ie if I want to study the 1s2s configuration I would set the first electron to the 1st eigenfunction and the second electron to the second eigenfunction.
Problem: This is probably a dumb question, but as far as I can tell, although the energies are right, the total solution doesn't seem close to normalized. I numerically integrated the radial portion as $$\int{r^2*\Psi^{*}*\Psi}dr$$ and got 0.1501 which, since the spherical portion of the hydrogen atom is 1 by design, means this doesn't seem to be normalized.
The paper, and other resources don't talk about it, but when doing numerical calculations do I need to worry about normalization of a wave function? I'd assume no, because in the end it's just a scaling number and should be calculable at the end of everything. Additionally, I tried to normalize my functions at different points in the code, and it actually caused convergence... at an energy of about 50 hartree for both electrons.
2. I initialize my electrons, and calculate my operator for both electrons individually using the above equation which is easy to implement in matlab. I can upload my code later, but I've checked it too many times at this point for the implementation to be the issue assuming the equations are right.
3. I use eigs function in MATLAB to solve for the lowest energy eigenvalues and eigenfunctions of the system to save time. For the ground state I'd only need to calculate the first one and for first excited I can calculate the first two (and use the second).
4. I compare the energy change of each electron individually and sum the total change to check for convergence using a 2-norm for the norm function. It's probably better to sum the energy of both electrons and compare it to the sum of the last energy instead, but looking at outputs, that wouldn't suddenly cause my code to converge and if it did, my energy values aren't matching what the paper got for helium.
4a. If I reach convergence I output the exact wave functions I found.
5. If convergence is not reached, I loop again with the electrons set to the new, calculated eigenfunctions where the 1s electron is set to the lowest energy solution of its operator and the 2s electron is set to the second lowest energy of its operator.
I can give more detail if needed, but it's easiest to skim through the paper.
The stepsize is 0.05 bohr out to 30 bohr radius which is low enough to generate a smooth function and avoid issues with missing oscillations of the wave. The wave also clearly converges for helium after ~10 bohr. Calculation speed isn't an issue either as that's essentially the reason the authors took this approach. The code as written in the paper, and in my code is also designed to easily scale to N electrons for higher Z nuclei. I just want to match the helium solution well enough.
I appreciate any help or discussion I can get. At this point I'm just trying to read what I can and try to better understand the numerical methods since I'm essentially just changing random things in my code hoping it works out.